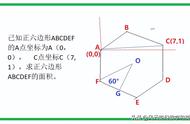
我们对蜂巢是六边形这件事已经习以为常,重来没有疑问为什么蜜蜂一定要将它建造成六边形?这件事本来也不需要解释,用哲学的观点来说就是存在即合理,这大概就是多数人的想法吧,可是有人就喜欢刨根问底,用我们学到的知识去解释自然现象,去了解蜜蜂们的智慧。其实运用小学二年级的数学知识就可以解释蜜蜂的“经济学”智慧。

蜂巢
蜜蜂的房子是用来储存蜂蜜或养育幼虫的,蜂巢一定是越宽敞越好。蜂巢越宽敞,能储存的蜂蜜越多,也越利于小蜜蜂的成长,可是筑巢又是一个非常消耗体力的活儿,蜜蜂需要将蜂蜡一点一点堆积形成蜂巢。蜂蜡则是以工蜂食用的蜂蜜为原料,在工蜂体内酝酿后,以蜡质的形式从工蜂腹部分泌出来的。工蜂用脚将蜂蜡一点点铺开,制成蜂巢的巢壁。每10克蜂蜡大约需要80克蜂蜜。采蜜是工蜂的职责,工蜂的寿命一般为1个月左右,一只工蜂一生中能采集的蜂蜜仅为4~6克,虽然每只工蜂能采集的蜂蜜少得可怜,但是它们有着庞大的数量,所以仍可以维持整个蜂巢的运转。蜂蜜既是蜜蜂的食物,也是筑造蜂巢的原料,所以对于蜜蜂来说,蜂蜜更显得弥足珍贵了,一丁点都不能浪费。所以蜜蜂在筑造蜂巢的时候必须考虑以下两个问题:
1、空间尽可能大
2、节约蜂蜜
我们在建造房子的时候会考虑在有限的预算内,尽可能造面积大的房子,蜜蜂也是这样,在筑巢的时候力求用最低的成本达到最大的舒适度。接下来我们将各种形状的蜂巢比对一下,再找到最优的形状。首先假设蜂巢是圆形的,从圆形蜂巢平面效果图上可以看出,如果蜂巢是圆形的,不管怎样排列,都会存在大量的空隙。

圆形排列
虽然对于周长相等的图形来说,圆形的面积最大,但是将蜂巢筑造成圆形的同时也产生了大量的空隙,这样做会浪费很多空间。
古希腊著名数学家毕达哥拉斯提出,在同一平面内用多个大小相同的基本图形进行拼接,能不留空隙的只有三角形、四边形和六边形三种。

多边形排列
因此,为了最大限度地利用空间,蜂巢的形状只能是三角形、四边形或六边形。如果想用有限的蜂蜡筑造面积尽可能大的蜂巢,就要选择在相等周长的前提下,用小学二年级学到的公式算一下各自的面积。
周长一定的情况下,所有三角形中,正三角形面积最大,假设周长是12cm,边长为4cm,三角形的面积(底*高÷2)为:
周长一定的情况下,所有四边形中,正方形面积最大,假设周长是12cm,边长为3cm,正方形的面积(边长*边长)为:
周长一定的情况下,所有六边形中,正六边形面积最大,假设周长是12cm,边长为2cm,正六边形的面积(边长*边长)为:
显然,在周长一定的情况下,上述三种形状中面积最大的是正六边形。在蜂蜡一定的情况下,将蜂巢筑造成六边形可以使横截面的面积达到最大。
六边形的房屋抗撞击能力强,非常结实,这种结构的产品质量轻、强度高,因而这种结构经常被用在飞机机翼、汽车车身及火车车门的设计中,为了让金属框架尽可能轻巧,在保证强度不降低的前提下,我们可以适当在框架上开孔。开孔可以减少金属的自重,为框架减负,而框架的强度主要由剩余(未开孔)部分来决定。但是,如果人们一味追求产品质量轻而大量开孔,势必会造成金属框架的强度不够。因此,保证产品强度是一个必要的前提,我们要在这个前提下尽可能地多开孔才能制成又轻又牢固的框架。

飞机机翼内部结构图
换个角度来思考,在用于支撑的金属量一定的条件下,使开孔的面积最大化,不仅可以保证产品的牢固度,还能尽可能减少质量。那么问题来了,开什么形状的孔最能满足上述需求呢?这次我们不是要筑造尽可能大的房间,而是要在金属表面开尽可能大的孔,但二者在数学上是一个原理。显然,我们要的是六边形的孔。所以,人们在制作强度高且质量轻的产品的时候,会用到蜂巢的六边形原理,将蜂巢的形状应用于最尖端的材料学当中。
突然发现数学真的不是枯燥、无趣的学科,如果当初我的数学老师像这样给我讲多边形的面积求解方法,我想我一定会爱上数学,可惜我是不能够重来了,数学需要科普,而不是简单的公式记忆!
,