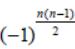a = np.array(
只要矩阵维度符合broadcasting要求,就可以用Numpy对矩阵和向量进行Hadamard乘积运算。

矩阵转置
神经网络经常处理维度不符合要求的矩阵。而矩阵转置提供了一种方法来“旋转”其中一个矩阵,以使其操作符合乘法要求。转置矩阵有两个步骤:
1.矩阵旋转90°
2.反转每行元素的顺序(例如[a b c]变为[c b a])
例如,将矩阵M转置为T:

a = np.array([
矩阵乘法
矩阵乘法规定了一组对矩阵进行乘法运算,以产生新矩阵的规则。
规则
并不是所有的矩阵都能进行乘法运算的。并且,对输出矩阵的维度也存在要求。参考资料
1.    第一矩阵的列数必须等于第二个矩阵的行数
2.  M×N矩阵和N×K矩阵的乘积是M×K矩阵。新矩阵取第一个矩阵的行和第二个矩阵的列。
步骤
矩阵乘法依赖于点积与行列元素的各种组合。以下图为例(取自Khan学院的线性代数课程),矩阵 C中的每个元素都是矩阵A中行与矩阵B中列的点积。

操作a1·b1表示我们取矩阵A中第一行(1,7)和矩阵B中第1列(3,5)的点积。