添加图片注释,不超过 140 字(可选)
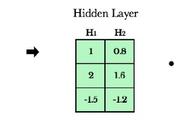
有非零解

添加图片注释,不超过 140 字(可选)
13、重要结论(需要掌握证明)
(1)设A是m×n阶矩阵,则齐次方程ATAx=0与Ax=0同解,r(ATA)=r(A)
(2)设A是m×n阶矩阵,r(A)=n,B是n×s阶矩阵,则齐次方程ABx=0与Bx=0同解,r(AB)=r(B)
5 特征值与特征向量
(一)矩阵的特征值与特征向量
1、特征值、特征向量的定义:
设A为n阶矩阵,如果存在数λ及非零列向量α,使得Aα=λα,称α是矩阵A属于特征值λ的特征向量。
2、特征多项式、特征方程的定义:
|λE-A|称为矩阵A的特征多项式(λ的n次多项式)。
|λE-A |=0称为矩阵A的特征方程(λ的n次方程)。
注:特征方程可以写为|A-λE|=0
3、重要结论:
(1)若α为齐次方程Ax=0的非零解,则Aα=0·α,即α为矩阵A特征值λ=0的特征向量
(2)A的各行元素和为k,则(1,1,…,1)T为特征值为k的特征向量。
(3)上(下)三角或主对角的矩阵的特征值为主对角线各元素。
4、总结:特征值与特征向量的求法
(1)A为抽象的:由定义或性质凑
(2)A为数字的:由特征方程法求解
5、特征方程法:
(1)解特征方程|λE-A|=0,得矩阵A的n个特征值λ1,λ2,…,λn
注:n次方程必须有n个根(可有多重根,写作λ1=λ2=…=λs=实数,不能省略)
(2)解齐次方程(λiE-A)=0,得属于特征值λi的线性无关的特征向量,即其基础解系(共n-r(λiE-A)个解)
6、性质:
(1)不同特征值的特征向量线性无关
(2)k重特征值最多k个线性无关的特征向量
1≤n-r(λiE-A)≤ki
(3)设A的特征值为λ1,λ2,…,λn,则|A|=Πλi,Σλi=Σaii
(4)当r(A)=1,即A=αβT,其中α,β均为n维非零列向量,则A的特征值为λ1=Σaii=αTβ=βTα,λ2=…=λn=0
(5)设α是矩阵A属于特征值λ的特征向量,则
A | f(A) | AT | A-1 | A* | P-1AP(相似) |
λ | f(λ) | λ | λ-1 | |A|λ-1 | λ |
α | α | / | α | α | P-1α |
(二)相似矩阵
7、相似矩阵的定义:
设A、B均为n阶矩阵,如果存在可逆矩阵P使得B=P-1AP,称A与B相似,记作A~B
8、相似矩阵的性质
(1)若A与B相似,则f(A)与f(B)相似
(2)若A与B相似,B与C相似,则A与C相似
(3)相似矩阵有相同的行列式、秩、特征多项式、特征方程、特征值、迹(即主对角线元素之和)
【推广】
(4)若A与B相似,则AB与BA相似,AT与BT相似,A-1与B-1相似,A*与B*也相似
(三)矩阵的相似对角化
9、相似对角化定义:
如果A与对角矩阵相似,即存在可逆矩阵P,使得P-1AP=Λ=

添加图片注释,不超过 140 字(可选)
,
称A可相似对角化。
注:Aαi=λiαi(αi≠0,由于P可逆),故P的每一列均为矩阵A的特征值λi的特征向量
10、相似对角化的充要条件
(1)A有n个线性无关的特征向量
(2)A的k重特征值有k个线性无关的特征向量
11、相似对角化的充分条件:
(1)A有n个不同的特征值(不同特征值的特征向量线性无关)
(2)A为实对称矩阵
12、重要结论:
(1)若A可相似对角化,则r(A)为非零特征值的个数,n-r(A)为零特征值的个数
(2)若A不可相似对角化,r(A)不一定为非零特征值的个数
(四)实对称矩阵
13、性质
(1)特征值全为实数
(2)不同特征值的特征向量正交
(3)A可相似对角化,即存在可逆矩阵P使得P-1AP=Λ
(4)A可正交相似对角化,即存在正交矩阵Q,使得Q-1AQ=QTAQ=Λ
6 二次型
(一)二次型及其标准形
1、二次型:
(1)一般形式
(2)矩阵形式(常用)
2、标准形:
如果二次型只含平方项,即f(x1,x2,…,xn)=d1x12 d2x22 … dnxn2
这样的二次型称为标准形(对角线)
3、二次型化为标准形的方法:
(1)配方法:
通过可逆线性变换x=Cy(C可逆),将二次型化为标准形。其中,可逆线性变换及标准形通过先配方再换元得到。
(2)正交变换法:
通过正交变换x=Qy,将二次型化为标准形λ1y12 λ2y22 … λnyn2
其中,λ1,λ2,…,λn 是A的n个特征值,Q为A的正交矩阵
注:正交矩阵Q不唯一,γi与λi 对应即可。
(二)惯性定理及规范形
4、定义:
正惯性指数:标准形中正平方项的个数称为正惯性指数,记为p;
负惯性指数:标准形中负平方项的个数称为负惯性指数,记为q;
规范形:f=z12 …zp2-zp 12-…-zp q2称为二次型的规范形。
5、惯性定理:
二次型无论选取怎样的可逆线性变换为标准形,其正负惯性指数不变。
注:(1)由于正负惯性指数不变,所以规范形唯一。
(2)p=正特征值的个数,q=负特征值的个数,p q=非零特征值的个数=r(A)
(三)合同矩阵
6、定义:
A、B均为n阶实对称矩阵,若存在可逆矩阵C,使得B=CTAC,称A与B合同
7、总结:n阶实对称矩阵A、B的关系
(1)A、B相似(B=P-1AP)相同的特征值
(2)A、B合同(B=CTAC)相同的正负惯性指数相同的正负特征值的个数
(3)A、B等价(B=PAQ)r(A)=r(B)
注:实对称矩阵相似必合同,合同必等价
(四)正定二次型与正定矩阵
8、正定的定义
二次型xTAx,如果任意x≠0,恒有xTAx>0,则称二次型正定,并称实对称矩阵A是正定矩阵。
9、n元二次型xTAx正定充要条件:
(1)A的正惯性指数为n
(2)A与E合同,即存在可逆矩阵C,使得A=CTC或CTAC=E
(3)A的特征值均大于0
(4)A的顺序主子式均大于0(k阶顺序主子式为前k行前k列的行列式)
10、n元二次型xTAx正定必要条件:
(1)aii>0
(2)|A|>0
11、总结:二次型xTAx正定判定(大题)
(1)A为数字:顺序主子式均大于0
(2)A为抽象:证A为实对称矩阵:AT=A;再由定义或特征值判定
12、重要结论:
(1)若A是正定矩阵,则kA(k>0),Ak,AT,A-1,A*正定
(2)若A、B均为正定矩阵,则A B正定