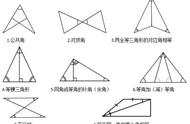
一、全等三角形证明条件归类:
从全等三角形证明的四种证明方法(边角边、角边角、角角边、边边边)来看:
①已知两边对应相等,第三个条件可以找已知两边的夹角对应相等 或 找第三边对应相等;
②已知两角对应相等,第三个条件可以找已知两个角的夹边对应相等 或 已知的两个角中的某个角的对应边相等;
③已知一边和一角对应相等,第三个条件可能是对应相等角的另一边对应相等 或 是另一角对应相等 。
综上:如何才能找到证明全等三角形的第三个条件呢?根据以上分析分为两种情况:
1、再找一组对应边相等;2、再找一组对应角相等。
二、对应边相等的情形:
1、公共边是第三个条件
例题1、如图,在△ABC 和 △ABD 中,AC = BD ,AD = BC ,求证 : △ABC ≌ △ABD

例题1图
证明:在 △ABD 和 △ BAC 中
∵ BD = AC , BC = AD , AB = BA (公共边)
∴ △ABC ≌ △ABD (SSS)
2、相等对应边 公共边的和 对应相等
例题2、如图,AB = CD ,AE = DF , CE = FB ,求证 :△ AEB ≌ △DFC

例题2图
证明:
∵ CE = FB ∴ CE EF = EF FB (即 CF = BE)
∵ AB = DC , AE = DF ,CF = BE
∴ △ AEB ≌ △DFC (SSS)
3、相等对应边 - 公共边的差 对应相等
例题3、如图,DF = CE , AD = BC , ∠D = ∠C , 求证:△AED ≌ △BFC

例题3图
证明:
∵ DF = CE ∴ DF - EF = CE - EF, 即 DE = CF
在 △AED 和 △BFC 中
∵ AD = BC , ∠D = ∠C ,DE = CF
∴ △AED ≌ △BFC (SAS)
4、等边三角形的三边相等(等腰三角形两腰相等)
例题4、如图, △ABC 和 △CDE 都是等边三角形 ,求证 :△ACD ≌ △BCE