4.其他辅助线做法
(1)延长已知边构造三角形
在一些求证三角形问题中,延长某两条线段(边)相交,构成一个封闭的图形,可找到更多的相等关系,有助于问题的解决.
例4.如图4,在△ABC中,AC=BC,∠B=90°,BD为∠ABC的平分线.若A点到直线BD的距离AD为a,求BE的长.

延长AD、BC交于F,
∵∠DAE ∠AED=90°,∠CBE ∠BEC=90°,∠AED=∠BEC,
∴∠DAE=∠CBE,
又∵∠ACF=∠BCE=90°,AC=BC,
∴△ACF≌△BCE,
∴BE=AF,
∵∠ABD=∠FBD,∠ADB=∠FDB=90°,BD=BD,
∴△ABD≌△FBD,
∴AD=FD=1/2AF, AD为a∴BE=2a
(2)连接四边形的对角线,把四边形的问题转化成为三角形来解决。
例如:如图8-1:AB∥CD,AD∥BC 求证:AB=CD。

分析:图为四边形,我们只学了三角形的有关知识,必须把它转化为三角形全等来解决。
(3)连接已知点,构造全等三角形
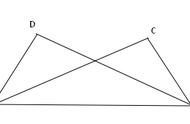
例如:已知:如图10-1;AC、BD相交于O点,且AB=DC,AC=BD,求证:∠A=∠D。

分析:要证∠A=∠D,可证它们所在的三角形△ABO和△DCO全等,而只有AB=DC和对顶角两个条件,差一个条件,,难以证其全等,只有另寻其它的三角形全等,由AB=DC,AC=BD,若连接BC,则△ABC和△DCB全等,所以,证得∠A=∠D。
(4)取线段中点构造全等三角形
例如:如图11-1:AB=DC,∠A=∠D 求证:∠ABC=∠DCB。