继续探究4.一边二角。
任意画△ABC,

同学们,可在草稿上用尺子作图。
一分钟过后......
通过画图,减下来是可以得到重合的。
可得两角和它们的夹边分别相等的两个三角形全等(简写成“角边角”或“ASA”)。
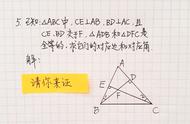
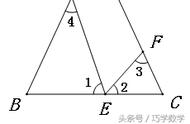
例3如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C,求证:AD=AE.

分析:
看题AD所在的是△ADC,AE所在的是△AEB,即证明△ADC≌△AEB
在△ADC和△AEB中
∠B=∠C
AB=AC
∠A=∠A
∴△ADC≌△AEB(ASA)
∴AD=AE

我们还可以得到两角和其中一个角的对边分别相等的两个三角形全等(简写成“角角边”或“AAS”)
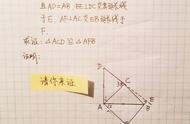
例4、如图,在△ABC和△DEF中,∠A=∠D,∠B=∠E,BC=EF.求证:△ABC≌△DEF

题中∠A=∠D,∠B=∠E,BC=EF,属于全等三角形判定的AAS。
在△ABC和△DEF中
∠A=∠D
∠B=∠E
BC=EF
∴△ABC≌△DEF(AAS)

总结:
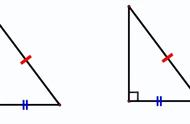
两角加一边分别都相等的两个三角形是全等,两角夹着一边分别相等两个三角形全等是简写成“ASA”,两角及一角的对边分别相等两个三角形全等是简写成“AAS”。
在确定判定全等是“AAS”还是“ASA”,一定看清楚是边是两角夹着,还是一角的对边。