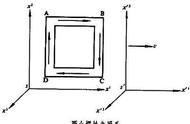
物体运动状态的改变往往牵涉两个因素,一是力,二是参考系。
现在先关闭第一个力的因素,当一个质点不受外力时,它的运动状态要想改变,只能通过改变参考系的运动状态,而这种质点运动状态的改变在物理上是不方便用数理方程去表达的,因为安装在参考系上的加速度计读数随时间呈复杂的变化特征,且这种变化特征使得理论物理学家们必须再次对该参考系本身进行研究。
现在再关闭第二个因素,当参考系不受外力时,安装在参考系上的加速度计读数为0,在此参考系下再次观察,会发现参考系不再改变被研究物体(质点)的运动状态了,要想改变质点的动量,只有给它施加力才能实现,牛顿第一定律说的就是这个事情,此时的参考系被称为惯性参考系,牛顿第一定律本质上是关闭了第二个因素,人为取定了一个零加速度参考系,让大家在这个参考系中进行动力学分析。 所以“惯性”二字如何理解,乃是在零加速度参考系中,物体(严格来说是质点)只要不受力,便习惯性的维持原来的运动状态!
严格来讲,没有不受力(合外力)的物体,无法完全关闭第二个因素,宇宙中所有惯性系均是近似的,均是为生产服务的。
选择惯性系的好处是,我不用再管参考系本身的动力学行为,我只需去研究质点系本身的动力学行为即可,相当于把地基作稳当了,然后开始盖房子。至此引出牛顿第二定律:质点动量的变化率等于作用在此质点上的力!见(1)式。

在给定的起始条件下,该方程式即可完全确定一个质点在时刻t时的位置,任何动力学方程的根本均是牛顿第二定律,而第二定律只在第一定律所定义的惯性系中成立。需强调,牛顿运动定律(含3大定律)是针对质点系的。