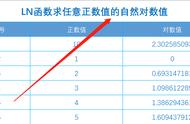
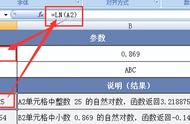
这个充满了噱头意味的标题,来源于我最近读过的两本书。一本是《小狗钱钱》,一本是《穷查理宝典》。也许是来自贫穷生活中的危机意识,让我想要开始研究经济和理财——而上述两本书,足以称得上是野生理财爱好者的入门经典。

《小狗钱钱》是一本关于理财的启蒙书,在惊叹于作者的想象力和文笔的同时,我十分后悔没有在15岁之前发现这样一本书。但只要你愿意,做任何事情都不算太迟,于是我赶在我的25岁,也就是2019年到来之前,很快把这本书读完了。书中提到了一个有趣的法则,叫做七二法则:
对于计算复利的一笔投资,在不追加投资也不取出投资的基础上,总金额达到原始金额两倍所需的年数,约等于72除以年平均利率。
举一个直观的例子就是,我们存了一笔定期存款,这个存款的年均利率是6%,那么七二法则告诉我们大约需要12年,存入的本金会翻番。很显然我们可以计算一下,(1 0.06)^12约等于2.01,这一法则的结论相当准确。
第一次读到这个部分的时候我脑中不假思索地给出了一个验证的步骤。这其实就是在求解一个关于年利率x、年数n的方程:
(1 x)^n = 2
方程基于复利列出,应当不难理解。如果你懂得高等数学里的泰勒公式,那么很显然存在一个粗浅的近似ln(1 x)≈x(事实上哪怕你只是一个高中生,也应当在数学题里见过无数次这个近似的式子,最起码在2012年之前江西省的高中数学题里我见过很多次)。于是上述的方程变成了:
n*ln(1 x)=ln2≈n*x
我在看书的时候并没有携带计算器,所以我直观地猜想,大概ln2 * 100的值约等于72吧,所谓的七二法则应该是这么近似推导出来的。

但是今天我发现事情并不简单。因为我回到宿舍,用计算器算出ln2的结果,大约是0.693。那么按照这一思路,所谓的七二法则应当变为六九法则才对。显然这个略显奇怪的名字并不足以准确描述问题本身,因为取数验算之后我发现七二明显是比六九更准确的。
问题出在哪里呢?
根据我以往的经验,精度上的问题,大多数都是泰勒展开式的项数太低。那么根据泰勒公式,在x=0附近有:
ln(1 x) = x – x^2 / 2 x^3 / 3 ……
我把更精确的近似式代入公式,发现根本无法直接计算,高次项的存在使得n与x之间的关系无法直接求解。
那么问题出在哪儿呢?起初我并没有想到合适的解释方法。直到我翻到《穷查理宝典》里的一篇演讲。《穷查理宝典》的主人公查理芒格是一位投资家,这本书可以认为是他的传记加作品集。提到他可能大多数人比较陌生,但他多年的合作伙伴一定让你如雷贯耳:沃伦巴菲特。而查理在巴菲特眼中,扮演的应当是导师和带头老大哥的角色。
在查理的一篇演讲稿中,提到了逆向思维。他在告诫一所高中的孩子们应当怎样规划人生的时候,恰恰是站在了“应当怎样让生活变得更糟”的角度。反着来,当问题反着来考虑的时候,往往能更高效地接近答案。
反着来,反着来,反着来。我念叨着查理的话,似乎在某一个瞬间想到了原问题的解释方法。既然利用之前泰勒近似行不通,那么首先回归原问题:
(1 x)^n = 2
反着考虑的话,假如说,我们首先认为七二原则是合理的,是否能推导出原问题两边的值近似相等呢?

答案是肯定的。首先等式的左边是最典型的牛顿二项式(如果你是一个合格的高中生,应当对这个名词不陌生),我们对其展开。考虑到x代表利率,是一个很小的数(比如5%,就是0.05,比1小得多),这一展开式近似写作:
(1 x)^n ≈ 1 n * x n * (n-1) * x^2 / 2 n * (n-1) * (n-2) * x^3 / 6 ……
反着想,那么我们把n * x * 100 ≈ 72作为已知条件!
为了让这个条件物尽其用,我们进一步简化近似!
(1 x)^n ≈ 1 n * x n * n * x^2 / 2 n * n * n * x^3 / 6 ……
那么代入这个反着想出的条件,我们得到:
(1 x)^n ≈ 1 0.72 (0.72)*(0.72)/2 (0.72)*(0.72)*(0.72)/6 = 2.041408

问题解决了!
我们借助逆向思维,用七二法则本身,加上牛顿二项式公式,推导出了上述的结果。等式的右边确实是一个非常接近2的数值。也就是说,不需要解原方程,我们确实“证明”了七二法则的合理性。
从这个例子我想到了两个问题。
其一,七二法则的适用场景。很显然,凡是可以用上述方程描述的场景,都能使用七二法则。也就是说,通货膨胀率也在七二法则的范畴里。简单来说,假如通胀率是8%,那么9年之后钱的购买力就只有一半了。啊,那么说到一二线城市底层劳动人民,假如保持通胀,而房价横盘保持不动,数年后也许更多人有信心买房了。房住不炒,房住不炒,希望贯彻原则,房价平稳着陆。
其二,逆向思维的重要性。也许是太久太久不做数学题,这个简单的问题竟然一时间难倒了我。这么想来,逆向思维确实在生活的方方面面都具有极其重要的价值,在很多时候能够化繁为简,切中要害。查理芒格能成为一代投资宗师,其理念必然有值得学习的地方。珍惜前人的智慧,恰恰是提升自我认知水准的不二法门。
,