各位同学大家好,让我们书接上篇继续认识二次函数经典的五大函数图像模板。


y=a(x-h)2 及y=a(x-h)2 k作为二次函数大家族的一员,其重要程度不言而喻。y=a(x-h)2 我们称为特殊顶点式,y=a(x-h)2 k称为顶点式。
什么是顶点式?
二次函数y=a(x-h)2 k,我们可以直接写出它的顶点坐标,坐标为(h,k)。
举例:
y=2(x-5)2 7,其顶点坐标为(5,7)
y=-3(x-3)2-9,其顶点坐标为(3,-9)
再看一下这个
y=-3(x 6)2-8,其顶点坐标为(-6,-8)
同学们考虑一下,这里的顶点坐标为什么不是(6,-8)?
注意二次函数顶点式y=a(x-h)2 k,(x-h)中间符号为“-”,这个式子y=-3(x 6)2-8可以理解为y=-3〔x-(-6)〕 2-8,同学们明白了吗?
而y=a(x-h)2是作为特殊的顶点式存在的,与y=a(x-h)2 k相比缺少常数项,即k=0,所以y=a(x-h)2的顶点坐标为(h,0)。
举例:
y=-2(x-5)2,其顶点坐标为(5,0)
y=3(x 6)2,其顶点坐标为(-6,0)。
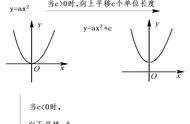
y=a(x-h)2 及y=a(x-h)2 k的熟悉运用对大家来说是非常重要的,一些题目中求解二次函数解析式,如果能给到二次函数图像的顶点坐标,那么我们利用这个公式会变得事半功倍。

y=ax2 bx c我们称为一般式。是二次函数的一般形式,具有明显的二次项、一次项及常数项。
有很多同学不太理解y=ax2 bx c一般式对称轴是怎么得到的。下面我们解析一下。
上文我们已经提到了二次函数y=a(x-h)2 k顶点式,已经明白了它的顶点坐标为(h,k),那么我们是不是可以把一般式y=ax2 bx c转化成y=a(x-h)2 k顶点式的形式?让我们尝试一下。