平行线的判定拓展延伸教案,平行线的判定习题课教学设计

课 题

平行线的判定

第 周

第 课时

教

学

目

标

1．掌握平行线的三种判定方法；

2．能够运用平行线的三种判定方法进行推理和计算．

教学重难点

重点：探索并掌握平行线的三种判定方法．

难点：探索两条直线平行的条件．

教学准备

课时安排

教 学 过 程

一、创设情景 明确目标

如图所示，装修工人正在向墙上钉木条，如果木条b与墙壁的边缘垂直，那么木条a与墙壁的边缘所夹的角为多少度时，才能使木条a与木条b平行？

二、自主学习 指向目标

自学教材第12至15页，请完成学生用书部分．

1．两条直线被第三条直线所截，如果__同位角__相等，那么这两条直线平行，简称为__同位角__相等，两直线平行．

2．两直线被第三条直线所截，如果__内错角__相等，那么这两条直线平行，简称为__内错角__相等，两直线平行．

3．两条直线被第三条直线所截，如果同旁内角__互补__，那么这两条直线平行，简称为同旁内角__互补__，两直线平行．

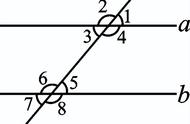
4．如图，直线a，b被直线l所截，若∠1＝__∠3__，则a∥b；若∠2＝__∠4__，则a∥b；若∠2＋__∠3__＝180°，则a∥b.

三、合作探究 达成目标

一 平行线的判定方法

活动1：

请同学们仔细阅读教材第13页“平行线判定的思考”，你知道在画平行线这一过程中，三角尺所起的作用吗？____________．

由此我们可以得到平行线的判定方法，如图．将下列空白补充完整(填1种就可以)

判定方法1(判定公理)__________________

几何语言表述为：∵∠________＝∠________

∴AB∥CD(　　　　)

由判定方法1，结合对顶角的性质，我们可以得到：判定方法2(判定定理)_____________________几何语言表述为：

∵∠________＝∠________

∴AB∥CD(　　　　)

由判定方法1，结合邻补角的性质，我们可以得到：判定方法3(判定定理)________________________________________________________________________

几何语言表述为：

∵∠________＋∠________＝180°

∴AB∥CD(　　　　)

展示点评：平行线的判定方法分别从同位角、内错角、同旁内角三个方面进行判别，前提是两条直线被第三条直线所截．

小组讨论：平行线的判定方法中的题设和结论各是什么？

反思小结：平行线的判定方法是已知条件是角的大小关系，结论是两条直线平行．

针对训练

1．如图，下列说法正确的是( D )

A．若∠1＝∠2，则c∥d B．若∠1＝∠3，则a∥b

C．若∠1＝∠4，则a∥b D．若∠1＝∠3，则c∥d