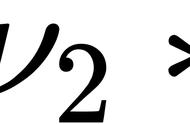平面向量的数量积是高考考查的热点和,主要以选择题、填空题为主考查数量积的概念、几何意义和坐标运算,属于中低档难度;主观题主要是以平面向量的数量积为工具与三角函数,解析几何等相联系解决与平面向量数量积有关的综合问题。
一、主干知识梳理:

二、典例精析:

【分析】由于向量AE与向量BD的长度和夹角都不知道,所以需要向已知长度和夹角的向量BA和向量BC转化或者建系利用坐标法求解;也可以考虑向量数量积的几何意义。
【解析】(1)方法一:基底法(化未知为已知):

方法二(坐标系法):连接AC,以AC,BD的交点O为坐标原点,OA,OB所在直线分别为x,y轴建立平面直角坐标系(图略),则