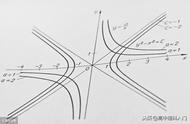
数学思想是数学的灵魂,是数学研究和解题的指导思想.在解决双曲线问题中最常用如下两种数学思想:
一、参数思想
双曲线中许多问题的解决,往往需要用参数表示某个点的坐标,然后根据题意自然约去参数.
例1(2021·广西玉林)如图,△ABC是等腰三角形,AB过原点O,底边BC//x轴,双曲线y=k/x过A,B 两点,过点C 作CD //y轴交双曲线于点D ,若S△BCD=8,则k的值是______.

【解析】依题意可知:点A和B关于坐标原点O对称,B和C的纵坐标相等,D和C的横坐标相等.因此,
引入参数a,设点A坐标为(a,k/a),则
点B坐标为(-a,-k/a),
点C坐标为(3a,-k/a),
然后得到点D得坐标为(3a,k/3a),
所以BC=3a-(-a)=4a,
DC=k/3a-(-k/a)=4k/3a,
由S△BCD=8,得:
1/2·4a·4k/3a=8,
整理,即得:k=3.
例2(2021·江苏宿迁)如图,点A、B在反比例函数y=k/x(k>0)的图像上,延长AB交x轴于C点,若△AOC的面积是12,且点B是AC的中点,则k=__________.

【解析】依题意,点B是AC的中点,所以点B的坐标可以由A、C的坐标所确定,因此引入参数a,b,设点A的坐标为(a,k/a),C(b,0),则由点B是AC的中点,得点B的坐标为((a b)/2,k/2a),
因为点B在双曲线y=k/x上,
所以(a b)/2·k/2a=k,
整理,得:b=3a,
所以点C的坐标为(3a,0),
因为△AOC的面积是12,
所以1/2·3a·k/a=12,
所以k=8.
例3(2021·湖北黄石)如图,A、B两点在反比例函数y=-3/x(x<0)的图象上,AB的延长线交x轴于点C,且AB=2BC,则△AOC的面积是___________.