转载:还记得被誉为“皇冠上的明珠”的哥德巴赫猜吗?这困扰了人类200多年的数学谜题,另无数数学家为之疯狂。另外,庞加莱猜想这个被称为21世纪七大数学难题之一,最后由两位来自中国的数学家完成了最后的攻坚。这是中国人对数学界的重大贡献之一。前有陈景润攻坚哥德巴赫猜想、后有朱熹平、曹怀东破解庞加莱猜想。但在此之外,诸如世界七大数学难题,它们就像一道道亮丽的风景,吸引着世界各国的数学家的注意。那么,世界七大数学难题究竟有哪些呢?
世界七大数学难题相关介绍

1、世界七大数学难题有哪些
这七个“世界难题”是:NP完全问题、霍奇猜想、庞加莱猜想、黎曼假设、杨·米尔斯理论、纳卫尔-斯托可方程、BSD猜想。这七个问题都被悬赏一百万美元。
2、23个数学难题
数学大师大卫·希尔伯特在1900年8月8日于巴黎召开的第二届世界数学家大会上的著名演讲中提出了23个数学难题。希尔伯特问题在过去百年中激发数学家的智慧,指引数学前进的方向,其对数学发展的影响和推动是巨大的,无法估量的。
20世纪是数学大发展的一个世纪。数学的许多重大难题得到完满解决, 如费马大定理的证明,有限单群分类工作的完成等, 从而使数学的基本理论得到空前发展。
2000年初美国克雷数学研究所的科学顾问委员会选定了七个“千年大奖问题”,克雷数学研究所的董事会决定建立七百万美元的大奖基金,每个“千年大奖问题”的解决都可获得一百万美元的奖励。
克雷数学研究所“千年大奖问题”的选定,其目的不是为了形成新世纪数学发展的新方向, 而是集中在对数学发展具有中心意义、数学家们梦寐以求而期待解决的重大难题。
3、世界七大数学难题的由来
2000年5月24日,千年数学会议在著名的法兰西学院举行。会上,97年菲尔兹奖获得者伽沃斯以“数学的重要性”为题作了演讲,其后,塔特和阿啼亚公布和介绍了这七个“千年大奖问题”。克雷数学研究所还邀请有关研究领域的专家对每一个问题进行了较详细的详述。克雷数学研究所对“千年大奖问题”的解决与获奖作了严格规定。每一个“千年大奖问题”获得解决并不能立即得奖。任何解决答案必须在具有世界声誉的数学杂志上发表两年后且得到数学界的认可,才有可能由克雷数学研究所的科学顾问委员会审查决定是否值得获得百万美元大奖。
其中有一个已被解决(庞加莱猜想,由俄罗斯数学家格里戈里·佩雷尔曼破解),还剩六个。
世界七大数学难题:NP完全问题

1、NP完全问题简介
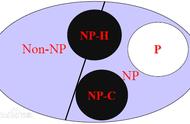
NP就是Non-deterministic Polynomial的问题,也即是多项式复杂程度的非确定性问题。
假设P ≠ NP的图解。若P = NP则三类相同。
假设P ≠ NP的图解。若P = NP则三类相同。
而如果任何一个NP问题都能通过一个多项式时间算法转换为某个NP问题,那么这个NP问题就称为NP完全问题(Non-deterministic Polynomial complete problem)。NP完全问题也叫做NPC问题。
2、NP完全问题的描述
例:在一个周六的晚上,你参加了一个盛大的晚会。由于感到局促不安,你想知道这一大厅中是否有你已经认识的人。宴会的主人向你提议说,你一定认识那位正在甜点盘附近角落的女士罗丝。不费一秒钟,你就能向那里扫视,并且发现宴会的主人是正确的。然而,如果没有这样的暗示,你就必须环顾整个大厅,一个个地审视每一个人,看是否有你认识的人。
生成问题的一个解通常比验证一个给定的解时间花费要多得多。这是这种一般现象的一个例子。与此类似的是,如果某人告诉你,数13717421可以写成两个较小的数的乘积,你可能不知道是否应该相信他,但是如果他告诉你它可以分解为3607乘上3803,那么你就可以用一个袖珍计算器容易验证这是对的。
人们发现,所有的完全多项式非确定性问题,都可以转换为一类叫做满足性问题的逻辑运算问题。既然这类问题的所有可能答案,都可以在多项式时间内计算,人们于是就猜想,是否这类问题,存在一个确定性算法,可以在多项式时间内,直接算出或是搜寻出正确的答案呢?这就是著名的NP=P?的猜想。不管我们编写程序是否灵巧,判定一个答案是可以很快利用内部知识来验证,还是没有这样的提示而需要花费大量时间来求解,被看作逻辑和计算机科学中最突出的问题之一。它是斯蒂文·考克于1971年陈述的。
3、NP完全问题的解决
人们发现,所有的完全多项式非确定性问题,都可以转换为一类叫做满足性问题的逻辑运算问题。既然这类问题的所有可能答案,都可以在多项式时间内计算,人们于是就猜想,是否这类问题存在一个确定性算法,可以在多项式时间内直接算出或是搜寻出正确的答案呢?这就是著名的NP=P?的猜想。解决这个猜想,无非两种可能,一种是找到一个这样的算法,只要针对某个特定NP完全问题找到一个算法,所有这类问题都可以迎刃而解了,因为他们可以转化为同一个问题。另外的一种可能,就是这样的算法是不存在的。那么就要从数学理论上证明它为什么不存在。
4、NP完全问题最新情况
2010年8月6日,HP LAB的 Vinay Deolalikar 教授宣布证明了P!=NP,证明文章已经发送到该问题各相关领域专家手中,等待检验,在他的主页上,证明过程已经公布(PDF格式共103页),但在8月15日,人们关于论文的看法——即证明不能成立——已经趋于稳定(当然这不能排除大家都同时犯了错误的可能性),随后的发言越来越多地集中于更抽象的层面,并且至今仍在继续。
世界七大数学难题:霍奇猜想

1、霍奇猜想简介
霍奇猜想是代数几何的一个重大的悬而未决的问题。它是关于非奇异复代数簇的代数拓扑和它由定义子簇的多项式方程所表述的几何的关联的猜想。它在霍奇的著述的一个结果中出现,他在1930至1940年间通过包含额外的结构丰富了德拉姆上同调的表述,这种结构出现于代数簇的情况(但不仅限于这种情况)。
2、霍奇猜想的描述
二十世纪的数学家们发现了研究复杂对象的形状的强有力的办法。基本想法是问在怎样的程度上,我们可以把给定对象的形状通过把维数不断增加的简单几何营造块粘合在一起来形成。这种技巧是变得如此有用,使得它可以用许多不同的方式来推广;最终导致一些强有力的工具,使数学家在对他们研究中所遇到的形形色色的对象进行分类时取得巨大的进展。不幸的是,在这一推广中,程序的几何出发点变得模糊起来。在某种意义下,必须加上某些没有任何几何解释的部件。霍奇猜想断言,对于所谓射影代数簇这种特别完美的空间类型来说,称作霍奇闭链的部件实际上是称作代数闭链的几何部件的(有理线性)组合。
3、霍金猜想的解决
黎曼假设、庞加莱猜想、霍奇猜想、贝赫和斯维讷通-戴尔猜想、纳维叶―斯托克斯方程、杨―米尔理论、P问题对NP问题被称为21世纪七大数学难题。2000年5月,美国的克莱数学研究所为每道题悬赏百万美元求解。目前,这一难题仍没有被破解。
对于(1,1)类的霍奇猜想已经在霍奇本人提出本猜想前的1924年由 Lefschetz证明。换句话说,霍奇猜想对于H^2成立。实际上,这是霍奇提出其猜想的动机之一。除此以外,还成立以下定理:如果霍奇猜想对于度数p的霍奇类成立,其中p<n,n是上述射影代数簇的维数,那么对于度数为2n-p的霍奇类,霍奇猜想也成立。
世界七大数学难题:庞加莱猜想