数学史上的十大难题:我猜你一个都不会做,会做说明你是数学大神!
数学,这门古老而又充满活力的学科,自古以来便吸引着无数智者去探索其深邃的奥秘。尽管数学领域已经取得了无数的辉煌成就,但仍有许多未解难题困扰着数学家们。这些难题不仅考验着人类的智慧,更推动着数学科学的不断进步。本文将介绍数学史上的十大未解难题,它们各自闪耀着智慧的光芒,等待着我们去揭示其背后的真相。

一、哥德巴赫猜想
哥德巴赫猜想是数学史上最著名的未解问题之一。它假设任何大于2的偶数都可以写成两个质数之和。尽管这个猜想看似简单,但数百年来,无数数学家试图证明或反驳它,却都未能取得突破性进展。哥德巴赫猜想的解决对于数论和数学分析等领域具有深远的影响,它将继续吸引着数学家们的关注和研究。
二、费马大定理
费马大定理是17世纪法国数学家费马提出的一个著名猜想,即不存在三个大于1的整数a、b和c,使得an=bn cn。这个定理的证明的过程历经了多个世纪,最终在1995年由英国数学家安德鲁·怀尔斯提出了完整的证明。费马大定理的解决不仅解决了数学史上的一大难题,也为数学研究提供了新的思路和方法。
三、黎曼猜想
黎曼猜想是关于素数分布的一个著名问题,它假设黎曼ζ函数的非平凡零点都位于复平面的临界线上。这个猜想对于解析数论、代数数论和数学物理等领域具有重要意义。尽管许多数学家试图证明或反驳黎曼猜想,但至今仍未取得突破性进展。

四、庞加莱猜想
庞加莱猜想是关于几何形状的一个基本问题,它假设三维空间中,任何封闭的三维形状都可以被连续地变换为球体。这个猜想在拓扑学中具有重要的地位,它的解决对于理解三维空间的性质具有重要意义。经过多位数学家的努力,庞加莱猜想最终在2003年被证明。
五、纳维尔-斯托克斯方程的存在性与光滑性
纳维尔-斯托克斯方程是描述流体运动的基本方程之一。这个方程的解的存在性和光滑性问题是数学和物理学领域的一个长期未解难题。尽管许多数学家试图解决这个问题,但至今仍未取得决定性进展。纳维尔-斯托克斯方程的存在性与光滑性问题的解决将有助于我们更好地理解流体的运动规律。
六、杨-米尔斯存在性和质量间隙
杨-米尔斯理论是粒子物理学中的基本理论之一,它描述了基本粒子的相互作用。然而,关于杨-米尔斯存在性和质量间隙的问题一直是数学物理领域的难题。这个问题涉及到量子场论和微分几何的深层次联系,其解决将有助于我们更深入地理解基本粒子的性质和行为。
七、贝赫和斯维讷通-戴尔猜想
贝赫和斯维讷通-戴尔猜想是关于椭圆曲线和模形式的一个著名问题。它假设对于任何给定的整数k,存在有限多个椭圆曲线,使得其L函数在s=k时的值为非零。这个猜想对于代数几何和数论等领域具有重要意义,它的解决将有助于我们更深入地理解椭圆曲线和模形式的性质。
八、霍奇猜想
霍奇猜想是关于代数几何的一个基本问题,它涉及到代数曲面的几何性质。这个猜想假设对于任何非奇异的复射影代数曲面,其霍奇线是代数的。霍奇猜想的解决将有助于我们更深入地理解代数曲面的几何结构,推动代数几何领域的发展。

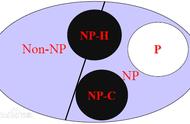
九、P对NP问题
P对NP问题是计算机科学和数学领域的一个基本问题。它涉及到计算复杂性和算法效率的问题。简单地说,P类问题是指那些存在多项式时间算法的问题,而NP类问题是指那些可以在多项式时间内验证解的问题。P对NP问题假设所有NP问题都是P问题,即所有可以在多项式时间内验证解的问题都存在多项式时间算法。这个问题的解决将有助于我们更好地理解计算复杂性的本质,推动计算机科学和数学领域的发展。
十、BSD猜想
BSD猜想是关于椭圆曲线和有限域的一个著名问题。它涉及到椭圆曲线的算术性质和几何性质之间的联系。BSD猜想假设对于任何给定的椭圆曲线E和有理数d,如果L(E,d)≠0,则存在阶为d的E的有理点。这个猜想的解决将有助于我们更深入地理解椭圆曲线的算术性质和几何性质,推动数论和代数几何领域的发展。
这十大未解难题在数学史上占据着重要的地位,它们各自闪耀着智慧的光芒,挑战着人类的智慧极限。虽然这些问题的解决需要漫长的时间和无数数学家的努力,但每一次的尝试和突破都将推动数学科学的进步和发展。我们有理由相信,在不久的将来,这些未解难题将会被一一攻克,人类将更深入地揭示数学世界的奥秘。