在高中数学函数中,我们常常会遇到关于奇偶函数的问题,不知道如何下手,今天我们就来讨论一下奇偶函数,看它是何方神圣,我们一起来揭开它的神圣面莎。
什么是偶函数呢?什么又是奇函数?
一般地,如果对于函数f(x)的定义域内任意的一个x,都有f(x)=f(-x),那么函数f(x)就叫做偶函数(Even Function)。
偶函数有何特点
- 定义域关于原点对称
- 值域关于y轴对称
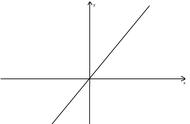
奇函数是指对于一个定义域关于原点对称的函数f(x)的定义域内任意一个x,都有f(-x)= - f(x),那么函数f(x)就叫做奇函数(odd function)。
奇函数的特点
- 奇函数图象关于原点(0,0)对称
- 奇函数定义域必须关于原点对称
- 奇函数在x=0处有意义,f(x)=0
- 设f(x)在定义域I上可导,若f(x)在I上为奇函数,则f′(x)在I上为偶函数。
以上就是对奇偶函数的定义以及特点进行归拿,面莎被一层一层的揭开,看清庐山真面目一切问题就变得简单了许多。
下面我们利用以上的知识来证明以下几个问题:
1. 两个奇函数相加所得的和或相减所得的差为奇函数。
2. 一个偶函数与一个奇函数相加所得的和或相减所得的差为非奇非偶函数。
3. 两个奇函数相乘所得的积或相除所得的商为偶函数。
4. 一个偶函数与一个奇函数相乘所得的积或相除所得的商为奇函数。
5. 当且仅当(定义域关于原点对称)时,
既是奇函数又是偶函数。奇函数在对称区间上的积分为零。
证明:
证明:①设f(x),g(x)在定义域R上为奇函数
∵f(x),g(x)在R上是奇函数
∴f(-x)=-f(x),g(x)=-g(-x)
令F(x)=f(x)+g(x)则F(-x)=f(-)+g(-x)
即F(-x)=-f(x)-g(x)=-F(x)
∴两个奇函数相加还是奇函数得证
对于其他的我就不一一的证明了,你们可以试试去证明
对于数学函数来说,要回到本来面目,回归原始,必带来很多方便,今天对于高中奇偶函数就解析到这,有什么疑问欢迎探讨。