角动量与物体的转动速度成正比
转动惯量又与物体的质量分布和转动半径有关,对于砖块来说,它的质量较大,并且在劈砖的过程中是围绕砖头的一边旋转,旋转半径较大,于是砖块会具有较大的转动惯量,因此在向下快速旋转的过程中角动量也比较大。

转动惯量与物体质量分布、旋转半径的关系
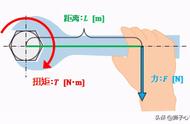
砖头在一边抬起之后,手掌劈向砖头的一侧,砖头将会绕着与桌面的接触点快速向下旋转,在旋转到与桌面平行的水平时,会撞击到桌面,桌面会给予旋转的砖头一个力矩的作用,前面讲过,力矩作用于旋转体时,会改变物体的旋转状态(相当于改变了物体的角动量),并且力矩越大,改变的速度越快(角动量变化速度越快),这个关系与牛顿第二定律非常相似。下面这个是关于力矩与角动量和作用时间的关系。

角动量在单位时间内的改变量等于力矩
如果我们将两边进行积分,就会得到下面这个公式。

在劈砖的过程中,力矩的作用时间非常短,因此,从开始撞击到撞击完所用的时间Δt=t2-t1非常小,而撞击前砖块的旋转速度为ω1,撞击桌面之后我们可以看做砖块的转动停止,转动速度ω2=0,从撞击前到撞击后,砖块角速度的改变量Δω=ω2-ω1= -ω1,在撞击的过程中,这个砖块的角动量改变量为-Jω1。
由于在撞击过程中的力矩是实时变化的,因此对于砖块的撞击,我们一般计算这个过程的平均力矩。