完全平方公式经典题,完全平方公式练习题初学

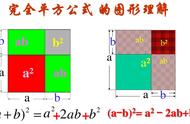
初中阶段共学三个乘法公式，分别是平方差公式，完全平方公式，十字相乘法。要求掌握并灵活应用的是平方并公式和完全平方公式，十字相乘法只需要能简单应用即可。今天我就用三个例题来给大家说说中考中是如何考查完全平方公式的。

例一图

上题是一年中考选择题，拿到题一看学生被如此大的数字吓倒了，再看a^2 b^2 c^2-ab-bc-ca，仿佛没有什么规律，所以学生觉得特别难。但是我们仔细观察发现a、b、c三者其实只相差1，我们就能想到a-b、b-c、c-a的值很小了，就能想到这些a-b、b-c、c-a就是完全平方的底数。再看a^2 b^2 c^2-ab-bc-ca就差-ab-bc-ca的2倍这种情况，很容易想到乘以2，得到1/2(2a^2 2b^2 2c^2-2ab-2bc-2ca),得到1/2[(a-b)^2 (b-c)^2 (c-a)^2]=3。

例二图

这道题应用完全平方比例一隐藏得更深，本题应用完全平方的目的是使计算简便，如果不用完全平方肯定计算要复杂得多。M=(x^2 2x 1)(x^2-2x 1)=[(x^2 1)^2-4x^2]=x^4 2x^2 1-4x^2=X^4-2x^2 1，N的计算也是一样的道理。

例三：整合各部分应用完全平方公式，也是经典题型。

例三图

此题很明显单个方程是无法解出a、b、c各自的值，也无法运用完全平方公式，只有把三个等式相加，得到a^2 b^2 c^2-2c 2b-6a=-11，(a^2-6a 9) (b^2-2b 1) (c^2-2c 1)=0，最终得出a、b、c的值。

上述三个例题，我已经将视频上传，如果还有不会的同学，可进入主页观看视频或者私信联系，谢谢关注。