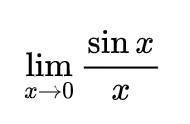在高中数学学习当中,洛必达法则就像一位神秘的向导,引导我们巧妙破解“0/0”和“∞/∞”这类极限难题。掌握这个法则,对于那些在高中数学甚至大学数学中挣扎的学生来说,洛必达法则无疑是一盏指路明灯。本文就从洛必达法则的证明过程,来剖析这个定理有如何妙用的地方.
洛必达法则的核心在于,当我们遇到“0/0”或“∞/∞”这类极限问题时,可以通过求导数的方式来找到答案。这个法则不仅让复杂问题变得简单,更教会我们如何用新的视角看待问题。
一: 洛必达法则定理表述
如果函数f(x)和g(x)满足以下条件:
1. 在点x=a的邻域内可导。
2. 。
3. ,或者f(x)和g(x)当时趋向于无穷大。
那么,如果极限存在或为无穷大,则:
二:证明过程:(详细推导)
1. 构造辅助函数:构造辅助函数h(x) = f(x) - mg(x),其中m是常数,使得h(a) = 0。
2. 泰勒展开:使用泰勒展开分析h(x)在x=a附近的行为。
3. 极限比较:通过比较f(x)和g(x)的极限,推导出洛必达法则。
洛必达法则证明
1. 构造辅助函数:设。构造h(x) = f(x) - Lg(x)。显然,h(a) = 0。
2. 泰勒展开:对h(x)在x=a处进行泰勒展开,得到:
由于h(a) = 0,上式简化为:
其中,。
3. 极限比较:由于h(x)在x=a处的极限为0,我们可以得到:
这意味着h'(a) = 0,即f'(a) = Lg'(a)。由此,我们得到:
这就完成了洛必达法则的证明。
结论
洛必达法则提供了一种处理形如“0/0”或“∞/∞”极限问题的方法,通过比较函数的导数极限来确定原函数的极限。这个证明过程展示了如何通过构造辅助函数和使用泰勒展开来推导出这个重要的微积分法则。
欢迎关注,支持转发,点赞,分享高中数学学习技巧