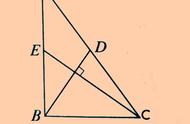
【题目】
如图1,在长方形ABCD中,点E是AD的中点,连接BE,点F是BE上的点,且EF=2FB,点G是AB上的点,且AG=3GB,连接GF并延长交CD于点H,已知长方形ABCD的面积是96平方厘米,求红色四边形DEFH的面积。

图1
【分析与解答】
题目要求红色四边形DEFH的面积,只告诉几条线段之间的关系及长方形的面积,并未告诉各边具体的长度,那就先找到红色四边形面积和长方形面积之间的关系再计算 。
连接GE,如图2。

图2
我们将三角形BFG的面积设为a,
因为EF=2FB,所以S△EFG=2 S△BFG=2a,则S△BEG=3a。
因为AG=3GB,即AB=4GB,
所以S△ABE=4 S△BEG=3a×4=12a。
又因为点E是AD的中点。
所以S矩=4 S△ABE=12a×4=48a。
如图3,

图3
过点E,作EP//AB,则P点是GH的中点,连接EH。
因为△EFP是△BFG按2:1放大的。
所以EP:GB=2:1,PF:FG=2:1。
即 S△EFP=2 S△EFG=2a×2=4a。
S△EPH= S△EPG=2a 4a=6a。
因为AG=3GB,我们将GB设为1份,则AG为3份,CD=AB=4份。
因为EP:GB=2:1,所以EP为2份。
如图4,

图4
延长GE,交CD延长线于点Q。则不难推出QH=2PE,即PH为4份。
因为点E为AD的中点,不难推出DQ=AG,即DQ为3份。
所以DH为1份。即DH=1/2EP。
所以S△DEH=1/2 S△EPH=6a÷2=3a。
所以S红= S△EFP S△EPH S△DEH=4a 6a 3a=13a。
所以红色四边形的面积是长方形面积的13a/(48a)=13/48。
所以红色四边形的面积是96×13/48=26(平方厘米)。
这个解法是不是太繁琐,你有什么好的解法呢?