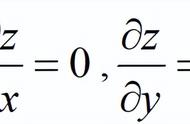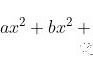最小二乘法(Least Squares Method)是一种常用的数学优化方法,用于拟合数据点与数学模型之间的关系。其目标是通过最小化数据点与模型之间的误差平方和,找到最佳的模型参数。
最小二乘法的基本原理是通过最小化误差平方和来确定模型参数。误差平方和定义为所有数据点的预测值与实际值之差的平方和。最小二乘法的目标是找到能够使误差平方和最小的模型参数。
在Python中,可以使用scipy库中的optimize模块的curve_fit函数来进行最小二乘法拟合。下面是一个使用最小二乘法拟合一条直线的简单示例:
import numpy as np
from scipy.optimize import curve_fit
# 定义要拟合的函数模型
def linear_func(x, a, b):
return a * x b
# 生成一些随机数据点
x_data = np.linspace(0, 10, 100)
y_data = 2 * x_data 1 np.random.normal(0, 1, 100)
# 使用最小二乘法拟合数据
params, covariance = curve_fit(linear_func, x_data, y_data)
# 输出拟合结果
print("拟合参数:", params)
在上面的例子中,我们定义了一个线性函数模型linear_func,然后生成了一些带有随机噪声的数据点。最后使用curve_fit函数进行最小二乘法拟合,得到了拟合参数params。
最小二乘法是一种常用的数据拟合方法,在实际应用中非常有用。它可以用于拟合各种不同类型的模型,例如线性模型、多项式模型、指数模型等。
最小二乘法的原理是通过最小化误差的平方和来拟合数据和数学模型之间的关系。它的基本思想是找到一组参数,使得数据与模型的预测值之间的差异最小化。
算法的优点:
1. 最小二乘法是一种简单且易于实现的算法。
2. 对于线性模型,最小二乘法具有闭式解,计算速度较快。
3. 最小二乘法对于数据中的噪声有一定的鲁棒性。
算法的缺点:
1. 最小二乘法对于异常值敏感,可能会导致拟合结果不准确。
2. 最小二乘法只能用于线性模型,对于非线性模型需要进行线性化处理。
3. 最小二乘法在数据量较大时,计算复杂度较高。
最小二乘法适用场景:
1. 数据与模型之间的关系是线性的。
2. 数据中的噪声较小,异常值较少。
如何优化最小二乘法:
1. 数据预处理:去除异常值或使用鲁棒性更好的方法处理异常值。
2. 非线性模型拟合:使用非线性回归方法,如多项式回归、指数回归等。
3. 正则化:引入正则化项来控制模型的复杂度,防止过拟合。
4. 加速计算:使用矩阵运算和并行计算等技术,提高计算效率。
5. 交叉验证:通过交叉验证选择最优的模型参数,提高模型的泛化能力。