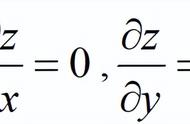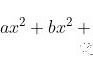最小二乘法的解释和例子
最小二乘是一种找到逼近一组数据的最佳直线的方法。
特别地,最小二乘寻求使每个数据点与预测值之间的差的平方最小化。这是一种线性回归,在工程和统计上应用广泛。

什么是最小二乘法?
最小二乘法寻求找到一条最接近一组数据的直线。 在这种情况下,“最佳”是指预测值和实际值之间的差的平方和最小的一条线。
为什么要用平方呢? 为什么不直接找到这些问题中预测值和实际值的差值之和呢?
在某些情况下,预测值会大于实际值,在某些情况下,预测值会小于实际值。 然而,在这两种情况下,预测值都是不准确的。
不过,只要找出差异,就会得到正负两种值的混合结果。 因此,仅仅把这些加起来并不能很好地反映两个值之间的实际位移。

然而,平方数总是正的。 因此,把这些加在一起可以更好地了解最佳拟合线的精度。
最小二乘法使用一个特定的公式来求直线y=mx b,使这个和最小。 实际上就是要找到一对m,b 的值,使得各点(x1, y1), (x2, y2), . . . , (xn, yn) 的纵坐标的平方和最小:

求解上述最小值时的m, b就得出直线y=mx b。
最小二乘法的定义
.
最小二乘法是一种寻找一条线来近似一组数据的方法,它使预测值和实际值之间的差的平方和最小。
这条直线的形式是y=b mx,其中m和b是使用给定数据集的x和y值计算的。
最小二乘法的公式
最小二乘方法的目标是找到一条方程y=mx b的直线,最接近数据。 这有时被称为最适合直线。
在这里,“最佳”意味着实际数据点和它们的预测值在直线上的差的平方和是最小的。 因此,有了“最小二乘”这个名字。
对于点为(x1,y1),…,(xn,yn)的一组数据,这条最小二乘线是y=mx b,其中m和b如下所示:
因为:y=mx b, 对于拟合的x 和 y有: