线性代数中的施密特正交化是使用一组基来构造标准正交基,要求基中的向量两两正交化。其核心思想就是从基中的两个向量开始,通过投影的方法逐对构造。想想二维空间中的两个线性无关向量,可以视为空间的一组基向量,将其中一个向量a向另一向量b投影,得到了a',可知a'与a是共线的与b构成了直角三角形的斜边与其中一条直角边,利用平行四边形法则c=b-a'就得到了与a正交的向量c一次,如果是多维空间可类推。
,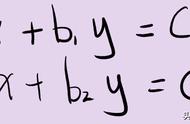
克莱姆法则介绍(克莱姆法则通俗易懂)
阅读全文>>2024-05-18 03:18:26

沃尔顿法则简介(沃尔森法则详细讲解)
阅读全文>>2024-05-18 03:23:10

迪米特法则大全(迪米特法则实例)
阅读全文>>2024-05-18 03:38:12

巴特莱法则介绍(沃克尔法则具体内容)
阅读全文>>2024-05-18 03:27:38

迪米特法则举例(克莱默法则的应用具体例子)
阅读全文>>2024-05-18 03:16:38

tryeverything歌词中英对照(tryeverything歌词中英文对照)
阅读全文>>2024-05-18 03:26:45

trytrytry歌词(歌词有try try try的英文歌)
阅读全文>>2024-05-18 03:32:04

数鸭子儿歌图谱(儿歌数鸭子节奏图谱)
阅读全文>>2024-05-18 03:24:51

袖手旁观歌词表达意思(袖手旁观这首歌表达的是什么意思)
阅读全文>>2024-05-18 03:13:41

袖手旁观歌词完整版(袖手旁观歌词)
阅读全文>>2024-05-18 03:25:03