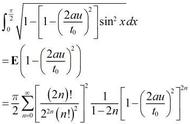xe^x的积分包括不定积分和定积分。不定积分求的是函数f(x)=xe^x的原函数,可以记为F(x) C,它是一个函数系统。而定积分求的是曲线f(x)=xe^x与x轴在区间[a,b]上,与x=a,和x=b围成的图形面积。

求定积分一般是建立在不定积分的基础上的,根据牛顿莱布尼兹公式,f(x)在区间[a,b]上的定积分等于F(b)-F(a). 因此我们先来探究如何求xe^x的不定积分,即求∫xe^xdx.
求不定积分一般基于常用的的积分公式,观察积分∫xe^xdx,可以找到近似的积分公式∫e^xdx=e^x C. 因为第一件事情,就是要把∫xe^xdx转化为含有∫e^xdx的式子。为了达到这个目的,需要进行如下两步变形:
1、凑微分,就是把e^xdx转化成de^x。即∫xe^xdx=∫xde^x。凑微分是最常用的积分方法,一定要掌握好。它的原理是微分的逆过程,即根据de^x=e^xdx,就有e^xdx=de^x. 不仅要掌握,而且要熟练常用的凑微分公式。比如cosxdx=dsinx, (secx)^2dx=dtanx, dx/x=dlnx等。
2、分部积分法,就是积分等于被积函数与微分变量的积减去被积函数和微分变量交换位置后的积分,即∫xde^x=xe^x-∫e^xdx. 虽然分部积分法有公式,不过如果能够用自己的语言把公式描述出来,运用上自然就不会有什么障碍了。因此老黄经常鼓励学生,要学会用自己的语言去描述定义、定理、法则和公式等。
现在就达到“把∫xe^xdx转化为含有∫e^xdx的式子”的目的了,并且可以利用基本积分公式,得到原函数的不定积分,其过程归纳如下:
∫xe^xdx=∫xde^x=xe^x-∫e^xdx=xe^x-e^x C=(x-1)e^x C=F(x) C.(最后的表示法是为了后面描述的方便)
在没有指定具体区间的情况下,我们取区间[a,b]上的定积分∫(a->b)xe^xdx=F(b)-F(a)=(b-1)e^b-(a-1)e^a.
如果加强理解,举一个具体的例子。假如求[0,1]上的定积分,则∫(0->1)xe^xdx=F(1)-F(0)=1. 即函数f(x)=xe^x,与x=1,以及两条坐标轴围成的图形面积为1.
现在你会求xe^x的积分了吗?
,