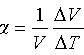其中 E(k) 是能量的傅里叶变换,ε 是单位时间内耗散的能量, k 是波数,具体过程如图。

▌Navier-Stokes 方程
一般认为Navier-Stokes 方程足以描述湍流,这个方程是流体的基本模型之一。

其中 u 代表速度,p 代表压强。第一个方程来自牛顿第二定律,第二个方程称为连续性方程,意义是不可压缩流体是连续的(物质不会凭空产生或消失)。值得注意的是对流项 (u·▽) u ,它代表惯性力,是方程非线性的来源,而粘性项 v △u 代表粘性力,可以说研究 N-S 方程性质就是判断这两项的搏斗谁会赢。物理学家引进了所谓雷诺数来描述速度场,即

根据雷诺数的大小,可以分为两种可能:
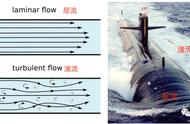
1. 雷诺数很小。这时粘性项占主导,动能会耗散殆尽,流体流动相当温和。
2. 雷诺数很大。这时对流项主导,湍流与激波产生,值得注意二维 N-S并不会产生湍流。
现在对N-S方程的研究成果表明,短时内N-S方程的解不会产生湍流,而这一结论是否可以拓展到长时尚不明确(目前想做到这一点需要加条件,这显然不是物理上能够让人满意的),上个世纪,一批数学家在假设速度场在有限时间爆炸的前提下对爆炸的集合(奇异集)进行刻画,发现奇异集在一定意义上是相当稀疏的,Mandelbrot 曾经猜测湍流会展现分形性质; 实际上, Scheffer 在表示, 这一定理正是受到 Mandelbrot 关于分形的论文的启发才证明的。有趣的事发生了,奇异集的豪斯多夫维数不大于5/3恰好与Kolmogorov理论中幂律的幂相同。以及,如果流体的速度场在某个时刻出现了爆破现象, 那么它的应力张量和涡量也同时会爆破. 于是流体内会出现应力非常大的点, 也会产生越来越不规则的漩涡. 这显然是湍流的重要特征。
陶哲轩研究了平均化的N-S 方程,目前的数学工具不足以区分它与真正的N-S 方程,而这个方程即使初值光滑,也会在有限时间爆炸(动能趋向无穷)。只要初值合适, 能量从大小大致为(1 ε0)−n(1 ε0)−n的漩涡向大小大致为(1 ε0)−n−1(1 ε0)−n−1的漩涡传递, 传递时间大致是(1 ε0)−5n/2(1 ε0)−5n/2, 而传递的比率大致是(1 ε0)5n/2(1 ε0)5n/2。有趣的事又发生了,他以数学角度严格重建了柯尔莫哥洛夫的K41理论,这种交会可能会指引我们找到答案。
最后,我想引用[1]中的一段结尾。
物理学一直在启发着数学, 但对于尚且没有准备好的数学家来说, 这种启迪总是很难参透. 自然界的基本规律用无声的语言向我们诉说, 而我们仍旧需要作出相当的努力去理解它.
"我还有好些事要告诉你们, 但你们尚且不能领会." ——[约翰福音 16:12]
▌后记
对数学方面感兴趣的读者可以学习[2],从推导直指前沿,本文主要参考[1],湍流方面的著作有[3],混沌与动力系统方面[4]是一本优秀易懂的教材。湍流图像来自视频 3Blue1Brown 可视化湍流,推荐。
[1]DTSIo,Navier-Stokes 方程的数学理论: 综述;
[2]Terence Tao ,254A-imcompressible fluid equations;
[3] Stephen B Pope, Turbulent Flows, Cambridge University Press,
[4] W.Hirsch, M., Smale, S., & L.Devaney, R. (n.d.). Differential Equations,Dynamical Systems&An Introduction to Chaos.