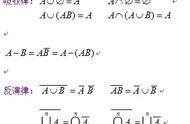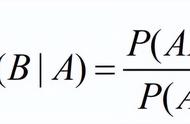这个系列讲讲我对概率论的理解。对,线性代数笔记的坑没填完,就开了新坑。首先感谢 @白草吧 和 @阿尔卑斯,在中的评论。我们学习任何数学知识,离不开讨论理解其几何意义和物理意义。好像是费曼说过,学物理要么有严密的数学推导,要么有清晰的物理图景。我们普通人通常没法在公式和数字中敏锐地洞察本质,但可以从几何和物理中探究概念的本质。这也正是我为什么首先感谢网友评论线性代数的文章。
本篇作为开篇,稍微讲一下概率论的基础。其实本系列也不会详细介绍概率论,原因之一就是对于工科来说,概率论这几百年前就开始发展的知识,如今已非常成熟,随便一本教材就写的足够详细。原因之二是我不是数学专业,再高深的高级概率论估计这辈子也没法理解了。所以本系列着重谈谈我对分布、密度函数和几个数字特征的理解,希望能抛砖引玉。
2 关于教材教材还是可以分为两类,一类是自上而下,由定义、定理、例题组成,通本来讲,没有特别的地方,就是一本词典型教材,大而全。这类教材随手拿一本即可,没有特别推荐的,我手头的就是高等教育出版社,宁荣健和朱士信主编的《概率论和数理统计》,选它是因为偶然在图书馆看到,里面的定义、定理排版清晰,随时翻阅较为省力。
第二类教材则相反,没有严格的讲述顺序,也没有繁多的例题,但对定义和定理有深入的介绍,适合有了基础之后再阅读,对一些概念往往一针见血、醍醐灌顶,我推荐中国科学技术大学出版社,陈希孺编著的《概率论与数理统计》。
3 关于如何学概率论概率论和另外两门数学,“微积分”和“线性代数”不同,特别是第一部分,随机事件和概率,我们学的时候往往有一种不和谐的感觉。这是由于概率的计算是基于集合的逻辑运算,而不是算术运算,所以好多算术运算法则,在计算概率的时候是不适用的,而且事件概率的表达式也并不唯一。
其次,虽然一般而言,教材在第一部分编排略少,但第一部分确是基础,主要分成:
- 几个重要概念,试验、事件、概率;
- 古典概型、几何概型、伯努利概型;
- 条件概率、贝叶斯公式。
古典概型对应了后面的离散变量,几何概型对应了后面的连续变量。条件概率和贝叶斯也是一个矛盾的两个方面,后续会展开陈述。
4 关于本系列开头说了,本系列不是大而全的详尽笔记,本系列会讲述5个方面:
- 条件概率和贝叶斯的矛盾统一;
- 密度函数的物理意义;
- 数学期望的物理意义;
- 方差的物理意义和几何意义;
- 协方差和相关系数的几何意义。