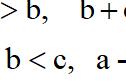老黄觉得,解三角形最重要的三个公式分别是:正弦公式、余弦公式和三角形的正弦面积公式,以及它们的变形公式。2022年新高考全国卷II的解三角形问题,就很好地结合了这三个重要公式。
记△ABC的内角A, B, C的对边分别为a, b, c, 以a, b, c为边长的三个正三角形的面积分别S1, S2, S3, 且S1-S2 S3=√3/2, sinB=1/3.
(1)求△ABC的面积.
(2)若sinAsinC=√2/3, 求b.
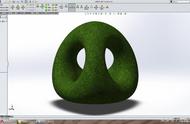
原题是没有图形的,老黄为了做个封面,就画了下面的图形,也能更直观地理解题目的条件和要求。我个你讲喔,要把这个图画准确,可比解这道题难多了哦。当然老黄也就画个草图而已。

分析:(1)题目的突破点之一,是利用三个正三角形的正弦面积公式,即S1=a^2sin60度/2, S2=b^2sin60度/2, S3=c^2sin60度/2, 利用题目所给的三个正三角形的面积关系,就可以转化得a^2-b^2 c^2=2. 因为上面所提到的三个公式都与边角有关,所以把面积关系转化成边的关系,会有更多的可能。
接下来利用角B的余弦公式:2accosB=a^2 c^2-b^2,就可以得到accosB=1.
下面判断角B是锐角还是钝角,因为要用到它的余弦,所以要判断角B的余弦的符号性质。因为b^2=a^2 c^2-2,即b比直角三角形勾股定理中的斜边相对要小,根据“小边对小角”,可以知道,角B是一个锐角。
因此cosB=√(−( )^)=2√/3, 这就可以求得ac=1/cosB=3√/4.
再次运用三角形ABC的正弦面积公式,就有S△ABC=acsinB/2=√/8.
(2)第二小题一看就知道要用到正弦公式:sinA/a=sinB/b=sinC/c. 然后分别用边的关系表示sinA和sinC. 就有边角关系sinAsinC=ac/(9b^2). 分子分母同时乘以cosB, 分子化为accosB=1,分母则化为9b^2cosB=6√b^2. 即1/(6√b^2)=√/3. 轻松解得b=1/2, 或b=-1/2(舍去).
下面组织解题过程:
解:(1)S1-S2 S3=(a^2-b^2 c^2)sin60度/2=√3/2,
a^2-b^2 c^2=2, 又a^2 c^2-b2=2accosB, ∴accosB=1,
由b^2=a^2 c^2-2, 知B<90度. cosB=√(1-(sinB)^2)=2√2/3,
△ABC的面积S=acsinB/2=ac/6=1/(6cosB)=√2/8.
(2)由sinA/a=sinB/b=sinC/c,有sinA=a/(3b), sinC=c/(3b).
sinAsinC=ac/(9b^2)=1/(9b^2cosB)=1/(6√2b^2)=√2/3.
解得: b=1/2, 或b=-1/2(舍去).
所以,解三角形的三个重要公式及其各种变形形式,你都掌握了吗?