接着说这本数学科普神作《从一到无穷大》

我们知道,一个数的平方,永远是正数,10的二次方是正100,负10的二次方还是正100。所以可以理所当然地认为,只有正数才有平方根,负数是没有平方根的。但数学家们在进行计算的时候,其实经常会碰到负数的平方根。比如说,有没有可能找出两个数字,让它们加起来等于10,乘积等于40呢?在实数范围内来看,答案是不存在的。但如果允许负数的平方根存在的话,那我们就可以找出一个答案,只不过这个答案中会包含根号-15这个奇怪的数字。数学家给负数的平方根起了个名字,跟实数相对应,叫虚数,还规定,根号-1叫i,这样的话,根号-20就是20i,根号-15就是15i。

但虚数这个东西,实在是看不出它有什么意义,所以即使它在数学计算里大量出现,数学家们一开始还是不承认它的名分。比如著名的数学家欧拉就说,虚数是想象出来的数,是不可能存在的,它们什么都不是,纯属虚幻。不过话虽这么说,欧拉该用虚数的时候还是用,因为实在没办法,不用的话,很多计算根本无法进行。

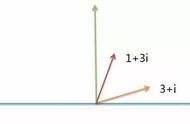
虚数的这种尴尬地位持续了整整有200多年,最后还是两个业余数学家给了它一个名分。这俩人一个是测绘员,一个是会计师,他俩从几何的角度,给虚数做了这样一个解释:你看啊,我们平常说的“数轴”,一般就是画一条横线,然后标上一个零点,左边是负数,右边是正数。那虚数如果要在数轴上找一个位置,应该怎么找呢?这两位说,在这条横线上,那肯定是找不到的,我们应该在零点处画一条跟横轴垂直的纵轴,也标上1、2、3、4……只不过这条线是代表虚数,所以其实是1i、2i、3i……这样一来,两条线组成一个坐标系,所有的数字,就都能在这个坐标系里找到了。比如15i,也就是根号-15,就在坐标轴里的纵轴上,如果是20 根号-15,那就在横轴上找到20,纵轴上找到15i,然后二者一交会,就能在坐标轴里找到这个数字。