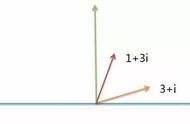
虚数
虚数这个概念经常让我感到困惑。就像是理解e一样,许多解释基本上都可以归为这两类:
· 这是一种数学抽象,这是方程式产生的结果,只管接受它就行了。
· 这个将用在高级物理中,相信我们吧,等你到了大学你就明白了。
专家们,这真是一种激励孩子们积极好学的方法啊!今天就让我们用我们最喜欢的工具来攻克它吧:
· 关注其中的关系,而不是机械化的方程式。
· 把复数当作我们原有数字系统的升级版,就像0,十进制和负数那样。
· 使用可视化的图表,而不只是文字,来理解这个概念。
还有我们的秘密武器:通过模拟来进行学习。我们通过对比它的先辈,负数,来进行学习。以下就是你的指南书:

看起来好像没什么意义,但是先把它放一边。到最后我们将先抓到它,然后再攻克它,而不是反之。
1.1 真正的理解负数
负数并不简单。假设你是18世纪的一名欧洲数学家。你有3和4,你知道4-3=1。很简单。
但是3-4呢?这,到底,意味着什么呢?你怎么能从3头奶牛中拿走4头?你怎么能拥有比空无一物更少的东西呢?
负数被认为是荒谬的,甚至被认为“导致整个数学都黯淡无光”(Francis Maseres,1759年)。但是在今天,认为负数符合逻辑或者是有用的并不荒谬。试着问问你的老师负数是否毁坏了数学的根基。
到底发生了什么呢?我们引入了一种有着一些有用性质的理论数字。我们摸不到,也抓不住负数,但是它很好的描述了一些确定的关系(比如债务)。这是一个很有用的虚构。
相比说“我欠你30元”,然后看看文字确认到底是你欠我还是我欠你,我可以直接写下“-30”,这样我就知道是我欠你了。如果我赚到了钱,还请了债务(-30 100=70),我可以很容易的记录这笔交易。我还剩下70元,这意味着我已经没有负债了。
正负标记可以自动的帮我们记录方向——你不要一一判断每笔交易。数学可以让这更简单,更优雅。负数是“有形还是无形”其实无所谓——它们有着一些有 用的性质,直到它们真正进入我们的生活我们才把它们发挥的淋漓尽致。如果你没有“得到”负数的话,你就会背上恶名(obscene name,应该是指美国的信用卡消费文化——译者注)。
但是我们不应自以为是:负数是一次智力的大飞跃。即使是欧拉,那位发现了e以及其他东西的天才数学家,也不像我们今天这样了解负数。负数被认为是“没有意义”的结果(最后他也随大流接受了这样的结果)。
这只是一个简单的证明,告诉我们今天的孩子们的智力应该可以更容易接受这些观点,即使这些观点曾经让很多数学前辈们很是困惑。
1.2 进入虚数的世界
虚数也有一个类似的故事。我们可以很轻易的解出以下方程:
x2 =9
答案是3和-3。但是加入有一个聪明人加入了一个小小的负号呢:
x2 =-9
哦。许多人第一次见到这个方程就退缩了。你想把一个比零还小的数字开平方,这是荒谬绝伦的。
这看起来很疯狂,就像负数,0,还有无理数(非重复数字)首次被引入时一样疯狂。这个方程并没有什么“实在”意义,对吧?
错了。所谓的“虚数”就像其他数字一样正常(即使它们也是被造出来的):它们是描述世界的一种工具。就像假设-1,0.3,0“真实存在”一样,让我们也假设一些i存在吧:
i2 =-1
这就是,你把i自乘两次就得到-1.接下来会发生什么呢?
首先我们会头疼。让我们玩个“假装i存在”的游戏吧,这样可以让数学更简单,更优雅。这样其中的关系就可以很容易的浮现出来了。
你或许不相信i的存在,就像那些老前辈们不相信-1的存在一样。现在是一个新的让我们难以理解的概念,现在还看不出有什么意义,即使是欧拉也没有。但是正如负数告诉我们的,怪异的概念一样可以有用。
我不喜欢“想象出来的数”这种称呼——这是一种设计好的侮辱,诽谤,故意伤害i的感情。i就像其他数字一样正常,但是“虚数”这个名字既然一直沿用下来了,我们只好继续使用。
1.3 以一种可视化的方法理解负数与复数
方程式x2 =9也可以表示成:
1·x2 =9
x应该是什么,使得它自乘两次后,1变成了9?
两个答案就是“x=3”与“x=-3”:这就是,你“乘以3”或者“乘以3,然后翻转”(翻转或取反是乘以负数的另一种解释)。
接下来让我们考虑以下x2 =-1,这其实就是:
1·x2 =-1
x应该是什么,可以使它自乘两次后,1变为-1?
· 我们不可能乘以一个正数,因为乘以正数以后还是正数
· 我们不能乘以一个负数两次,因为相乘两次后又会变为正数。
但如果是……旋转呢!这听起来很疯狂,但是如果我们假设x被“转过了90度”,然后乘以x两次那就是旋转180度,也就是把1翻转成了-1!

耶!让我们继续深入考虑下去,我们可以把它绕其他方向旋转(比如说顺时针方向)来从1变为-1.这就是“负向”旋转或者是称作乘以-i:

如果我们乘以-i两次,我们把1变成-i,然后-i变成-1,所以-1确实存在两个根:i与-i。
这个很酷。我们有一些答案,但是这说明了什么呢?
· i是一个“新的想象出来的维度”,来标记数字
· i(或者-i)就是指数字“被旋转”
· 乘以i就是沿逆时针方向旋转90度
· 乘以-i就是沿顺势正方向旋转90度
· 无论那个方向,旋转两次就是-1:这就把我带回到“传统”的正负维度上去了。
数字是二维的。是的,这样可能有些难以理解,这就像让古罗马人理解十进制与长除法一样(你说1和2之间还有数字是什么意思?)。
我们会问“怎样通过两步,把1变成-1”,然后我们就找到了答案:把它旋转90度。这确实是一个奇怪但是又让我们耳目一新的方法来理解数学。而且它很有用。(顺便提一下,这种用几何的方法解释复数的方法直到i被发现几十年后才被引入)
此外,逆时针为正是人们的一个约定俗成习惯——其他表示也是可以的。
1.4 发现其中的模式
让我继续深入细节。当我们连续乘以负数时(比如说-1),你就得到一种模式:
1,-1,1,-1,1,-1……
因为-1并不改变数的大小,只改变符号,你就这样的反复进行翻转。比如说数“x”,你就会得到:
x,-x,x,-x,x,-x……
这个点子很有用。x可以代表好的或坏的发型。假设每周都轮流变换;这周是好发型周,那么47周会是什么周呢?
x·-147 =x·-1=-x
那么-x就意味着坏发型周。注意到负数是怎样“保持符号的轨迹的”——我们可以直接在计算器中输入“-147 ”而不用一步一步计算(1周是好的,2周是坏的,三周是好的…………)。通过运用负数这一切只是反复翻转而已。
Ok。现在让我们看看如果乘以i后会发生什么?
1,i,i2 ,i3 ,i4 ,i5 ……
非常搞笑。让我们化简一下:
· 1=1(毫无疑问)
· i=i(已经很简单了)
· i2 =-1(这是i的定义)
· i3 = (i·i)·i=-1·i=-i(啊哈,逆时针旋转3次=一次旋转,很简单)
· i4 = (i·i)·(i·i) =-1·-1=1(四次旋转就是一个完整的圆)
· i5 = i4 · 1=i(接下来再来一次)
用图表示出来就是: