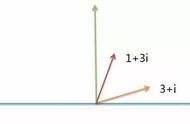
每四次旋转循环一次。这就有意义了,对吧?小孩子都可以告诉你旋转四次跟没有旋转一样。与其关注虚数(i,i2 ),不如看看更一般的模式:
X,Y,-X,-Y,X,Y,-X,-Y……
就像负数一样翻转,虚数可以模仿任何在两个维度之间旋转的东西。或者是任何遵循周期或环形关系的东西——你想到些什么了吗?
cos与sin,如果你没有想到的话,后面我们还会提到于这个有关的棣美弗定理(De Moivre Theorem)[编辑注:Kalid正在接受电击治疗以治疗他喜爱使用双关语]
1.5 理解复数
这里还有另外一个细节需要揭示:一个数字可以既是“实的”又是“虚的”吗?
确实能。谁说我们必须旋转90度?如果我们一只脚在实数范围内,另一只在虚数范围内,就像这样:

我们处在45度角的为止,实数部分的大小与虚数部分的大小相当(1 i)。这就像一个热狗既有芥末酱也有西红柿酱——谁说你只能选一种的?
事实上,我们可以任意选取实数与虚数组成一个三角形。角度就是“旋转的度数”。复(合)数就是给这种数字准备的一个相当完美的名字。它们写作 a bi,其中
· a是实数部分
· b是虚数部分

目前为止还不错。但是还有最后一个问题:复数有多“大”呢?我们不能单独测量实数部分或是虚数部分,因为我们忽略了整体。
让我们再退回去看看。负数的大小不是指你能把它数到多少——而是它距离零点的距离。因此负数的距离就是负数的平方再开根。
这是另一种计算绝对值大小的方法。但是对于复数,我们在90度的时候我们怎么测量两部分?
这是只鸟……这是飞机……这是毕达哥拉斯!
老天啊,他的理论真是到处都有,即使是在他2000年以后发明的数字中。对,我们构造一些三角形,然后斜边就是它到零点的距离:
a bi的大小等于a与b平方和再开根
非常干凈。虽然计算复数的大小并不像负数那样去掉负号就可以了,但是它有它的用处。让我们来看一看。
1.6 示例:旋转
我们不会等到去大学物理中学习虚数。我们现在就学学吧。关于复数相乘有很多内容,但是把这个切记于心中:
乘以一个复数就是绕着它旋转
让我们先来看一看。假设我在一艘小船上,船头的指向是向东3个单位,向北四个单位。我想把船头指向逆时针旋转45度。新的指向可以快速画出来吗?

有些能人会说“很简单嘛,用正余弦函数,切线Blahblah……消去变量什么的……”真要命。对不起,我打断你的计算了吗?能再回答一次这个问题吗?
让我试一种更简单的方法:我们的指向是3 4i(无所谓角度是什么,我们并不关心),然后我们想旋转45度角。那么45度角就是1 i,那么我们乘以它就好了!