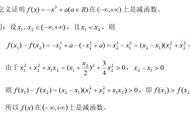单调性与单调区间
函数单调性:如果函数f(x)在某个区间上是增函数或减函数,那么就说函数f(x)在该区间上具有单调性。
单调区间:函数对应在某区间内具有单调性,这个区间就是它的单调区间。
图像特点:单调区间内,增函数的图像是上升的,减函数的图像是下降的。
学会了没有,拿一道题检验一下就知道了!

例题一“图像法”
图像法求解函数单调性问题:就是直接根据函数单调性对应图像的特点来解决问题。
直接看图可知:
在区间【-5,-2】内,函数图像呈现下降趋势,所以在该区间内是单调减函数;
在区间【-2,1】内,函数图像呈现上升趋势,所以在该区间内是单调增函数;
在区间【1,3】和【3,5】你应该会判断了吧!
这是在已知函数图像的情况下解答,如果函数图像未知怎么办?别急,我们还有最有效的办法-“定义法”。定义法就是直接按照函数单调性定义来求解。

定义法求函数单调性问题
定义法: 判定函数在某个区间上的单调性的方法步骤:
1. 设x1, x2∈给定的区间,且x1<x2;
2. 计算f(x1)-f(x2) 至最简;
3. 判断上述差的符号;
4.判断。(若差<0,则为增函数; 若差>0,则为减函数).
同样的,学没学会,来道题一练便知!

定义法求解函数单调性问题
题和解题过程在上图中已经给出,我就不再赘述了。
好了,今天的课程内容就那么多,你学会了吗?
让欧阳老师再给你总结一下今天到底学习了哪些内容!