鸡兔同笼需要知道四要素,鸡兔同笼最简单方法为什么

鸡兔同笼问题是小学数学人教版教材中四年级的内容，而且是知识广角里的内容。

当然，作为国民级的应用题，中国小学生提前接触鸡兔同笼很正常，我就见过有的老师在孩子一二年级的时候就开始讲这类问题了。

我是在小学生三年级的时候开始讲鸡兔同笼问题的，也算是稍微提前一点儿吧。

鸡兔同笼问题的解法有很多种，我总结了十几种方法，不过提问者问的是给二年级的孩子讲鸡兔同笼问题，我想了一下，可能以下两种方法比较适合。

鸡、兔在同一个笼子里，上面有35个头，下面有94只脚。问：鸡、兔各多少只？

第一种，列表法

这种做法看起来比较“笨”，但是却有它的优点，具体的解决办法就是一个一个的数，一个一个地试。

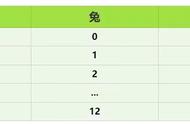
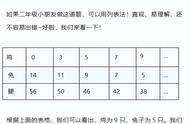
首先列一个表格，在表格中可以看到，鸡和兔子的脚数不同，所以，对于不同只数的鸡和兔子，虽然它们的总数相等（都等于35只），但是脚数是变化的，我们将不同组合下的鸡和兔子的脚数分别列出来，以表格的形式展示如下：

列表的时候，我们先假设鸡有35只，那么兔子就只能是0只，这样就算出了总的脚数，然后将鸡的只数递减，兔子的只数递增，依次计算出总的脚数，最终能够计算出当鸡有23只，兔子有12只时，总脚数等于94只，符合题目中的条件，进而得到最终的结果。

实际上，在填写表格的时候，也不需要完全把所有的结果都计算出来，只需要填写几个空格，细心的同学通过观察数字的变化规律，就可以很轻松的判断出鸡和兔子的只数了。

很多学生和家长对这种方法不屑一顾，觉得这种方法既笨拙又麻烦，我并不这么认为，其实，对于小学低年级的学生而言，这种方法我倒是认为是最值得推荐的方法，因为在制作表格的过程中，学生需要自主地去探索鸡、兔在数量变化的时候，总脚数的变化特点，通过动手绘制以及用眼观察，分析比较得出，由于兔子的脚比鸡多两只，所以当鸡数少1只，兔数多1只的时候，总脚数会增加2只的规律性认识。而这正是培养学生探索精神，提升学生数学思维的重要途径。

第二种，假设法

鸡兔同笼的解法中，我个人最喜欢的同时也是最推荐学生使用的就是假设法，因为假设法几乎能够解决所有类型的鸡兔同笼问题，即使题目进行了很大的改编和变形，假设法都能有效的对题目进行解析，当然，对于一些变形的鸡兔同笼问题，用假设法会比较烧脑。在实际应用中，假设法几乎是最经典，最有效率的一种方法，学生运用假设，将不同的情形（鸡和兔子的脚数不同）转化成相同的情形，有利于简化问题，理清思路。

鸡兔同笼问题的难点就在于每只鸡和每只兔子的脚数是不同的，这是问题的难点，但也是解决问题的关键点或者说是突破口，假设鸡和兔子的脚数相同，那么，题目就会大大简化，将复杂问题简单化，是解决数学问题的常见思路。

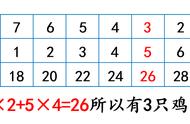
假设一：所有兔子都站起来，藏起2只脚。这样的话，每只鸡和每只兔子的脚数就相等了，都是2只，在这种情况下，一共有35个头，也就是说一共有35只动物，每个动物有2只脚，那么总的脚数=35×2=70只，这比题目给出的94只脚少了24只，想一想为什么少了？因为每只兔子都站了起来，收起了2只脚，一只兔子少2只脚，一共少了24只脚，所以一共有24÷2=12只兔子，再用35-12=23就是鸡的数量。

假设二：我们也可以把鸡假设成兔子，此时，所有鸡增加2只脚。这样的话，每只鸡和每只兔子的脚数就相等了，（都是4只），在这种情况下，一共有35个头，也就是说一共有35只动物，每个动物有4只脚，那么总的脚数=35×4=140只，这比题目给出的94只脚多了46只，想一想为什么这次脚又多了呢？因为每只鸡都多了2只脚，一只鸡多2只脚，一共多了46只脚，所以一共有46÷2=23只鸡，再用35-23=12就是兔子的数量。

实际上，假设法不仅能做出经典的鸡兔同笼问题，对于一些鸡兔同笼变形题，包括分组法解决的鸡兔同笼问题，都能很好地解决，大家要不断地用假设法去尝试解决这类问题。

其他的诸如抬脚法，巧妙是很巧妙，但孩子听了后也很可能无法展开应用，方程法在这个阶段给他们讲，对他们训练数学思维没有什么好处，这里就不展开了。