"欧拉公式" 是一个数学公式,表示为 e^(ix) = cos(x) i*sin(x)。它是由欧拉提出的,是复数数学和微积分学的重要公式之一。

首先,欧拉公式的两边都是复数的指数形式。e是自然常数,其值约为2.718,i是虚数单位,表示根号-1。右边的公式则是指数展开后的复数形式。
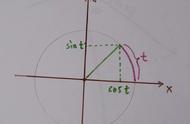
其次,欧拉公式揭示了复数与三角函数之间的关系。可以看出,复数e^(ix)的模为1,它的指数为ix,可以表示为cos(x) isin(x),即欧拉公式的右边式。这个公式等价于e^(ix) = cos(x) - isin(x),也称作欧拉公式的另一种形式。
最后,欧拉公式在微积分学和数学物理学中有着重要的应用。它是许多复数积分和微积分等高级数学问题的基础公式,在科学和工程领域中都有着广泛应用。
总之,欧拉公式是一个重要的数学公式,它揭示了复数与三角函数之间的关系,并在微积分学和数学物理学中有着重要应用。这个公式不仅有理论意义,也具有实际意义,是数学中的重要公式之一。
在更高级的数学中, 欧拉公式还有其他推广,比如欧拉公式的推广,Euler's Formula for Complex Exponentials,它是一个关于欧拉公式的更一般形式。其中,cis(x) = cos(x) i*sin(x),这种形式广泛应用于电学、电子学和信号处理等领域。
欧拉公式也与欧拉函数有关,欧拉函数是一类复数函数,其中一个重要的性质是,e^(ix) = cos(x) i*sin(x), 它们在解析函数理论和复数分析学中有着重要应用。
总之,欧拉公式是一个重要的数学公式,它在数学、物理学、工程学等多个领域有着重要的应用。它不仅是复数数学中的基础公式,也是微积分学和数学物理学中重要的理论工具。欧拉公式揭示了复数与三角函数之间的关系,这个关系在许多科学和工程领域中都有着重要应用。欧拉公式的推广和欧拉函数的概念也在很多领域中有着广泛的应用,是数学和工程学中重要的理论基础。
,