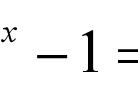欧拉恒等式
二阶微分方程明显比一阶难了很多,下面三图详细地对二阶常系数齐次线性方程的通解进行了推导。



有几下几点需要注意:
1、理解思路。
求二阶常系数齐次线性方程的解,一开始是靠猜的,因为以e为底数的指数函数,不论多少次求导,相差的都是常数系数,天然符合二阶常系数齐次线性方程。所以,我们先假定方程的解是一个e为底的指数函数,然后代回原方程反解出来这个函数,那么这个函数就是方程的解。
2、特征方程。
特征方程是假定好方程的解然后代回方程反解过程中产生的,因为方程是二阶的,所以出现了一个二次方程作为特征方程。
3、常数变易法。
当特征方程有两个相同实根的时候,相当于只求出了一个原方程的特解,所以需要使用常数变易法来再求一个特解。常数变异法简单说,就是把解中的常数换成函数,代回原方程反解出来这个函数,从而得到方程的解。一句话,猜解的结构,然后代回原方程反解出这个结构中未知的部分,得到方程解。
4、欧拉公式。
指数为复数的运算就得靠它了,著名的欧拉恒等式就能从它推导出来(彩图中的等式)。这是第一次在学习中涉及它。
,