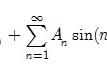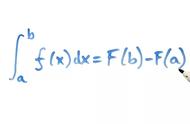图四
图四是连续函数 的图形从 到 这一段与 轴之间的面积, 在 这一点, 函数 是高度, 面积以函数 表示。牛顿的想法是求面积函数 在 点的瞬间变率。欲求 的瞬间变率, 必须先求平均变率, 因此牛顿考虑下面的图五(并见注三)。当 变化到 时, 从 到 的面积是 而 就是图五中在 上方的面积, 因此平均变率等于。如果函数 在 上是常数的话, 则 这块面积是一个以 为高度的长方形, 如图六所示:


在图六的情形, 不论 的大小, 都等于长方形面积 的高, 令, 自然得到 对 的瞬间变率是此长方形的高, 即。
一般而言面积 这一块并非长方形而是形如图七:

图七
在图七中, 令 和 分别是函数 在 上的最大值和最小值, 则显然有(注四)
当 时, 和 都会趋近, 因此 也会趋近, 亦即 对 的瞬间变率是, 或者说。这就是当年牛顿发现的微积分基本定理(注五)。
根据此一定理, 我们有下列结论:
如图二所示, 令 满足, 则图二中的面积等于。原因是, 因为如图四, , 如果 也等于, 则, 是一个常数(注六)。图二中的面积等于, 注意到, 所以
(向左滑动查看完整公式)
虽然满足微分是 的函数并不唯一, 但是因为这些“反微分”彼此只差一个常数, 在计算 时, 所差的常数自然会对消, 因此并不重要(注七)。
以下, 我们补充当 不一定恒正时图四中的面积函数 应该如何定义。如图八, 当 在某一区段小于0 时, 从 到, 阴影部份的面积若是除以, 得到的“高度”是正的, 而非 (此处), 因此一个合理的面积函数 在图八中应该计以负值, 如此, 而 也小于0, 并且当 时, 会趋近于, 也小于0。