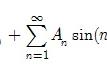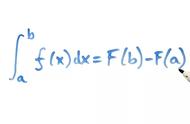图八
如此一来, 只要将 时的“面积”计以负值, 则微积分基本定理仍然成立, 如图九

图九
函数 有正有负, 当 时阴影部分面积以正计之, 而 时阴影部分面积以负计之, 则总面积仍然会等于, 是 的反微分(注八)。
换句话说, 只要将 的部份, 面积以负计, 则微积分基本定理仍然成立(利用 的任一个反微分, 图九的阴影部份“面积”皆等于)。读者不妨试试下面这个函数, 其在 这一段的“面积”计算。

图十
若以反微分 代1 和-1 相减,
(向左滑动查看完整公式)
恰是图十中阴影部分面积取负号。
总之, 微分是求函数图形切线的斜率, 积分是求图形与 轴之间的“面积”, 这面积两字需要打一引号,来说明“面积”是要考虑正负的。唯有如此, 微积分基本定理才会广泛的成立。因此, 可能如注八, 得到“面积”为0 时, 原因不过是正的面积和负的面积对消, 一点也不奇怪。
注一:, 以便处理 函数图形与 轴之间的面积,将来,当 时, 会引进“负的面积”的概念。并见注八。
注二:代表一个微小的量,可正可负,但是不能等于0,本文为了方便说明,均大于0。
注三:莫里斯⋅克莱因着古今数学思想(Morris Kline,Mathematical Thought Frome Ancient to Modern Times)中译本第69页重现了牛顿所画的图

图中的记号"0" 相当于现在的。
注四:在闭区间 上有最大值和最小值,并且当 时, 最大和最小值均趋近 。
注五:一般认为莱布尼兹亦独立发现此定理。
注六:的函数统称是 的反微分或反导函数, 的所有反微分彼此只差一个常数,图五中的面积函数 是 的一个特别的反微分,它满足 。
注七:多项式 的反微分是 , 是任意常数。三角函数 的反微分是, 是任意常数。下面二个函数图形阴影部份的面积分别是 和。