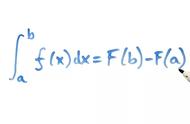《简明微积分》这本书,是华罗庚的弟子——龚昇先生的一本名著。这本书最早的版本,于1965年,在中国科学技术大学近代物理系试验班,作为教材试用。目前已经出到第四版,高等教育出版社。在amzon上,可以找到我对第四版的书评,署名是xxxxxxxx,还可以找到更多的书评。
先说一下我接触这本书的过程,这几乎是一个巧合。
2010年我博士毕业,进入山东科技大学担任教师,教自动化、电气工程、应用物理等专业的一些电工基础课程。比如《电路原理》这门课程,不同的系科也叫《电路基础》、《电路分析》《电工学1》。
作为工科基础课的教师,必须熟练掌握微积分、微分方程、线性代数、复变函数与积分变换的基础知识。另外,根据师门遗风,师祖建议,基础课教师的数学水平,应该不低于前苏联斯米尔诺夫的《高等数学教程》,这本书基本上包括、甚至超出了工科、物理的所有传统高等数学知识。而由于《教程》这本书早已绝版,所以我毕业后不得不寻找替代的读物。我在毕业之前,已经读过了前苏联菲赫金哥尔茨的《微积分学教程》,以及十几部线性代数和矩阵,所有很自信“懂”微积分。
后来由于阴差阳错的原因,在网上偶然看到龚昇先生本人的讲座,用外微分讲微积分的基本原理,我感觉醍醐灌顶,深受教育。并且立刻意识到,其实自己根本就是一知半解,微积分根本没入门。更谈不上能在我的课程里运用微积分的思想和概念。龚昇先生本人的讲座,现在网上仍然可以搜到。所有学微积分、但没学过外微分的读者,我都强烈建议去读这部《简明微积分》。我在图书馆先看过几次,感觉实在有必要,就买了一本。为此我曾两个晚上连续通宵。工科和物理的书,完全可以引人入胜,就看作者有没有这个能力和水平。
著名数学家吴文俊先生为这本书写了序,引几句给各位看看。......通过Newton与Leibniz之手,.....认识到微分与积分是互逆的两个概念,.....统一成微积分基本定理。......法国数学家H.J.Poincare指出了多重微积分应该有一个正负定向。......使多重积分在坐标变换下原来有些拖泥带水的变换公式,有了一个精炼的形式,并使Newton——Leibniz微积分基本定理到多变量的推广,步入了坦途。(------注:就是Newton——Leibniz、格林、高斯、斯托克斯四个公式可以写成一个stokes公式。)H.J.Poincare关于体积元有定向这一发现,导致了外微分形式的出现。......定向是几何拓扑中最有深刻意义的的伟大创造之一。......龚昇教授以其敏锐的目光指出了微积分的核心是单变量的Newton——Leibniz微积分基本定理以及多变量的Stokes公式,可谓切中要害,并使高等院校的初学者得以轻松地登堂入室。.....在汗牛充栋的微积分教程中,占有特殊的位置。
下面是我的一些体会。
《简明》与通常的课本,比如同济《高数》很不同。
《简明》在第5页就开始了定积分,然后第18页开始微分,前30页就已经讲完了微分中值定理和微积分基本定理。真是能让初学者大开眼界,非一般的教学水平。稍后的泰勒展开、近似计算也很精彩。紧接着非常顺畅地,介绍了工科根本不教的,微分方程解的存在性和唯一性定理(这是在求解微分方程之前必须考察的,只有有解,你才有可能去求;只有解唯一,你才能说你找到了那个解,或者去逼近那个解)。这个定理我在硕士的时候,用了两个星期才看懂什么意思。当时这个定理对我的学习影响很大,直接引导我进入了非线性系统理论的学习。
《简明》后来很轻松地介绍了Jacobi矩阵,这个很重要,就是坐标换元法的意思,基本上会在所有微积分的应用中明显地或者隐含着地出现,比如初等概率论中求正态随机变量的变换等等。
最最精彩的莫过于第七章,线、面积分与外微分形式,龚昇先生以完全初等水平的知识,轻松阐明了格林、高斯、斯托克斯公式形式上、思想上都是Newton——Leibniz微积分基本定理的推广:他们统统是,函数在高维区域的积分与原函数在低维(高维的边界)的积分这两个东西的关系。这一章,你还可以学到为什么三维空间只能定义梯度、旋度、和散度。以及高水平的——一般在微分几何中,比如在微分流形中——才出现的重要的H.J.Poincare引理及其逆。
第九章,一致连续性、Darbou和,函数的可积性(就是你什么时候才能算积分!!!)。
第十章也够精彩。这一章你能学到审敛法的Dirichlet定理和Abel定理。对我影响很大的一个思想是,数列、、函数、级数、广义积分完全可以看成是一回事。这使得我在学习实分析和泛函分析的时候,减少了很多思想上的、逻辑上的困难。
最后一章是傅里叶级数,虽然精彩,但是对工科和物理系,比如电气电子要学习电磁场,感觉不够,我想你应该去读专门的偏微分方程或者数学物理。
《简明》一书,主题分明,一气呵成,读此书宛如听龚昇先生本人的讲解。由于《简明》大大地提高了我对数学的认识和好奇心,极大地影响了我的教学和工作,我愿意将此书推荐给所有对高等数学有需求的读者。
最后要说明一点,“学什么”这件事,或许是你践行“活到老学到老”这一准则的大问题,但是初学者根本没有能力考虑自己该学什么,或许只能阴差阳错地“胡乱”做一个决定。不过,能知道自己学了什么,这些东西到底什么意思,是不是退而求其次的好态度呢?读懂《简明》,基本上,你已经做好了微积分入门的准备。随着见识的积累、能力的增长,比如Rudin的《数学分析原理》(我曾用这本书教过工科硕士三次)等等国际名著,已经在向你招手了,而你可能走向更加了解自己、更加相信科学的道路。
感谢阅读。我是菜鸡速通理工基础,欢迎关注
,