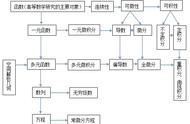
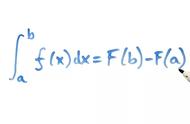微积分是高等代数的入门基础,必须掌握的知识。要理解微积分,必须先了解为什么需要微积分,这样才能更好的的掌握。

微积分发展,一般认为经历了三个阶段,第一个阶段是极限概念,这个概念其实很早以前就被提出了,比如说中国古代的庄子、古希腊的阿基米德等均提出过极限的概念。第二个阶段是求积的无限小阶段,这个阶段也在很久前被提出,如我国著名的数学文献《九章算术》就提出圆形分割求面积法。第三个阶段则是微积分互逆关系,最后一个阶段是由牛顿、莱布尼兹完成的。如果说前面两个阶段是萌芽阶段,那么在第三阶段就是发展成熟阶段,最终发展出现代高等代数的基础——微积分学。

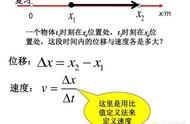
微分的几何意义,如函数y=f(x)的图形是一条曲线,并且函数是可微的,曲线上一点M的坐标是[x0,y0],那么如果P发生了一点变化,变成了N点,也就是横坐标增量为△x时,对应纵坐标的增量为△y。

通过M点做一条切线T,曲线上N点在T线上对应的点为P点,P点的横坐标也为x0 △x,纵坐标为y0 dy,也就是说,相对M点而言,T线上发生增量△x对应纵坐标的增量为dy。如果△x很小,小到MN段曲线可以认为是一条直线,一条经过M点的且和切线T重合的直线,那么这时候就可以认为△y无限接近于dy。
这下就好办了,如果曲线上任何一点都可以变化为切线来求,也就是说微分是一个“以直代曲”的思想,那么问题就变得很简单了,这便是微分的几何意义。