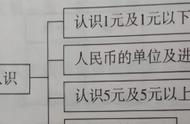
四年级下册︱教材在小数的认识和加减法单元,将原“小数的意义”和“测量活动”调整为 “小数的意义(一)”“小数的意义(二)”“小数的意义(三)”,这样做的目的是什么?
本册的“小数的意义”是在三年级结合实际情境初步认识小数的基础上,从一般意义上对小数意义的再认识,其关键是要在小数与十进分数、整数之间建立起联系。教材这样调整的价值主要体现在以下几点:
首先,教材通过调整,将小数意义的学习设计为逐层递进的四个课时,即:
第一课时,旨在借助元角分、长度原型和直观模型使学生体会到小数与十进分数之间的关系;
第二课时,旨在扩大小数的应用背景,加深学生对小数的理解;
第三、四课时,旨在认识小数数位的名称及它们之间的关系,借助计数器介绍小数部分的数位名称及数位的相互关系,使学生进一步理解小数的意义。
通过安排这四个课时,将小数意义的认识拓展到生活中更广泛的领域,帮助学生有层次地理解小数的意义。
其次,教材从不同角度为学生提供了多个实物原型和直观模型,从而帮助学生更好地理解小数,其具体表现如下:
(1)在小数的意义(一)中,教材呈现了元角分、长度原型和分数直观模型;
(2)在小数的意义(二)中,通过测量引入直尺的直观模型,即引入了数线;
(3)在小数的意义(三)中,呈现了数位顺序表。
这些原型和直观模型对于学生体会小数与十进分数的关系,以及认识小数各个数位的位值意义,发挥了重要的作用。

五年级下册︱整数乘分数与分数乘整数的意义相同吗?
在以往的教学中,分数的意义很明确,几个几分之几就用分数乘整数,一个数的几分之几则用整数乘分数,但在五年级下册教材第22页“分数乘法(一)”中,3个1/5是多少,是用整数乘分数来列式,这样是不是表明整数乘分数与分数乘整数的意义相同呢?
这实际上是乘法算式是否要区分“被乘数”和“乘数”的问题。根据《义务教育数学课程标准(实验稿)》及《课程标准(2011年版)》,小学数学教材中已经不再区分乘数和被乘数。例如在整数乘法的运算中,算式“4×6”既可以表示6个4相加,又可以表示4个6相加,即在不涉及具体问题情境下,可以代表两个意义,4×6=6 6 6 6或4×6=4 4 4 4 4 4都是对的。反过来,6 6 6 6既可以写成4×6,也可以写成6×4。同理,4 4 4 4 4 4 既可以用4×6表示,也可以用6×4表示。也就是一种意义可以用两种方式表示。但在具体应用问题的情境中,不同的算式可以表示相同的含义,比如“有6个小朋友,每人有4支铅笔,一共有多少支铅笔?”,要解决这个问题,可以列出算式4×6或6×4,但实际的意义都是表示 6个4相加。
在解决实际问题教学过程时,教师要注意让学生理解各数的意义,鼓励他们用自己的语言表达算式的具体含义,但列成算式不要区分“被乘数”和“乘数”,即不要强调“被乘数” 和“乘数”书写位置上的人为规定。同样,在分数乘法的内容中,教材也不区分乘数的位置,处理方法和整数一样,也就是说分数乘整数不但可以表示几个相同分数的和,还可以表示一个数的几分之几是多少。
这样的处理,不仅符合课程标准的精神,同时也减少了学生在学习中的“人为”障碍。学生在学习乘法时最重要的是体会乘法的意义,如果过分强调“被乘数”和“乘数”的区别,一是使学生将主要精力放在了这种区分上,可能造成对乘法的意义学习的忽略;二是区分二者对学生来说一直是难点,这加重了学生不必要的学习负担,很多学生是能够在具体情境中运用乘法正确地解决问题,却因为“被乘数”和“乘数”的顺序问题而导致“出错”。
在运算教学中,教师要让学生经历从实际情境中抽象出运算的过程,要关注学生对运算意义的理解过程。教师要帮助学生建立实际问题与数学运算的内在联系,使学生通过解决实际问题,产生直觉经验,找到数的运算的现实背景,促进学生理解运算的含义及其性质,并能自觉地运用于解决应用问题之中。在教材中,无论是对“分数乘法”的学习还是其他运算的学习,都十分重视加强学生对运算意义的理解。
需要指出的是,目前市场上有一些练习册,由于不了解我们的编写理念,会出现类似“3×1/5和1/5×3的意义、算法、结果是否相同”这样的题目,这不是一个好题目,建议教师给予学生正确的引导,不要让学生在这些问题上浪费太多的时间。
在回答这个问题的同时,笔者看到了上海市浦东新区教育学院曹培英老师的一篇文章《关于乘法运算意义与乘法交换律的教学处理》,很受启发。文章在最后谈到的一段文字非常有道理,特摘录部分内容与大家分享:
事实上,面对用情境图或文字表达的实际问题,如:

共 ?只或 “每袋有6只橘子,4袋一共有几只橘子?”
学生一般都能分清6×4或 4×6中的6表示每袋6只橘子,4表示有4袋。但再进一步要求学生概括:“这是求4个6,而不是求6个4”,就会有学生感到困难。于是,为了帮助这些学生,引进了各种各样的练习(包括所谓的“文字题”),越练越“玄”,越练要求越高……以往教学中,教学要求把握失当,也是造成或者扩大“人为教学障碍”的重要因素之一。因此,正确定位“乘法初步认识”的教学目标,是解决问题的一条配套措施。否则,即使从一开始就让学生认识乘法的可交换性,并取消书写位置的限制,仍会存在“人为的教学障碍”。

六年级下册︱为什么教材鼓励学生经历“类比猜想—验证说明”的过程,探索圆柱和圆锥体积的计算方法?
我们以圆柱体积的内容安排为例。教材安排了探索圆柱体积计算方法的内容,引导学生经历“类比猜想—验证说明”的探索过程,体会类比、转化等数学思想方法。教材先呈现了“类比猜想”的过程,由于圆柱和长方体、正方体都是直柱体,而且长方体与正方体的体积都等于“底面积×高”,由此可以产生猜想:圆柱体积的计算方法也可能是“底面积×高”。在形成猜想后,教材又引导学生“验证说明”自己的猜想。教材中呈现了两种“验证说明” 的方法:一种是用硬币堆成一堆,用堆的过程来说明“底面积×高”计算圆柱体积的道理,这实际上是“积分”思想的渗透;另一种方法是“转化”思想的渗透,即把圆柱通过“切、拼”转化为长方体,再根据长方体体积的计算方法推导出圆柱体积的计算方法。
要求让学生经历“类比猜想—验证说明”来探索体积计算方法的过程,主要是由于这样的学习过程的重要性。数学发现通常都是在类比、归纳等方法进行探索的基础上,获得对有关问题的结论或解决方法的猜想,然后再设法证明或否定猜想,进而达到解决问题的目的。当然,通过合情推理得到的猜想还需要进一步证明。在小学阶段不要求给出严格的证明,只要学生能够从不同角度说明其合理性即可,可以说是验证说明。
所谓类比,就是由两个对象的某些相同或相似的性质,推断它们在其他性质上也有可能相同或相似的一种推理形式。运用类比的关键是寻找一个合适的类比对象。圆柱和圆锥的体积与已学习过的长方体和正方体的体积存在诸多相似点,为进行类比提供了良好的基础。可能在学习长方体和正方体的体积时,学生已经初步理解了体积和容积的含义,掌握了长方体和正方体的体积计算方法,这些知识都是学习圆柱体积的基础,特别是长方体和正方体的体积计算公式“底面积×高”对探索圆柱的体积计算方法有正迁移作用。这就使得圆柱和圆锥的体积学习有了合适的类比对象或者说类比的基础。
,