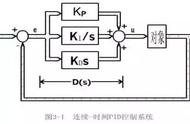
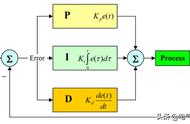
d

e
下面举一个现场整定的例子。在某塔顶温度调节系统中,被调参数是塔顶温度,工艺允
许波动为<4℃,调节参数是回流量。在整定过程中,考虑到对象滞后较大,反应较慢的情况,δ的选择从50%开始凑试起,此时在阶跃作 用下(给定值降低2%)的过渡过程曲线见图5-(a)。此时调节时间长,不起振荡,于是将比例度减少,δ=30%、20%、及10%时的曲线见(b)、(c)、(d)。显然,20%的情况最好,衰减比接近4:1,Ts=10分。
按4:1衰减曲线法数据表定出整定参数:
δ=0.8·δs=16%;
Ti=0.3·Ts=3分;
Td=0.1·Ts=1分。
投运时,先将δ放在较大的数值,把Ti从大减少到3分,把Td从小到大逐步放
大到1分,然后把δ拉到15%,(如果在δ=15%的条件下很快地把Td放到1分,调节器的输
出会剧烈变化)。再对系统加2% 的给定值变化时,仍产生4:1衰减过程,见图(e)所示,调节质量显著改善,超调量小于1℃,调节时间为6.5分。
3 经验试凑法
这是在生产实践中所总结出来的方法,目前应用最为广泛,其步骤简述如下:
1)、根据不同调节系统的特点,先把P、I、D各参数放在基本合适的数值上,这些数值
是由大量实践经验总结得来的(按4:1衰减),其范围大致如表4所示。但也有特殊情况超出表列的范围,例如有的温度调节系统积分时间长达15分钟以上,有的流量系统的比例度可到200%左右等等。

2)、看曲线,调参数,根据操作经验,看曲线的形状,直接在闭合的调节系统中逐步反复试凑,一直得到满意数据。
在实践中,把具体整定的方法总结了几段顺口溜。
参数整定找最佳,从大到小顺次查,
先是比例后积分,最后才把微分加;
曲线振荡很频繁,比例度值要放大,
曲线漂浮绕大弯,比例度值应减小;
曲线偏离回复慢,积分时间往下降,
曲线振荡周期长,积分时间再加长;
曲线振荡频率快,先把微分降下来,
动差大来波动慢,微分时间应加长;
理想曲线两个波,前高后低四比一,
一看二调多分析,调节质量不会低。
第一段讲的是整定顺序,δ和Ti都是从大到小逐步加上去,微分是最后才考虑的。
第二段讲的是比例度如何整定。
第三段讲的是积分时间如何整定。
第四段讲的是微分时间如何整定。
第五段讲的是标准。
上面这种方法步骤是先加δ,再加Ti,最后才加Td。应用中较稳妥。
另一种方法是先从表列范围内取Ti的某个数值,如果需要微分,则取Td=(1/3~1/4)Ti,然后对δ进行试凑,也能较快地达到要求。
实践证明,在一定范围内适当地组合δ和Ti的数值,可以得到同样衰减比的曲线,就是说,δ的减少,可以用增加Ti的办法来补偿,而基本上不影响调节过程的质量。所以,这种情况,先确定Ti、Td再确定δ的顺序也是可以的。而且可能更快些。如果曲线仍然不理想,可用Ti、Td再加以适当调整。另外,将所在装置控制系统的PID参数记录下来,是一个很好的做法。
3)、在不熟悉的生产过程中,应先进行手动调节。进入自动调节时,应确定比例度、积分时间、微分时间。当调节输出变化一点点而影响测量值有较大变化的这种场合,为考虑到系统的稳定性,应加大比例度,反之,则减小比例度。当调节器的输出变化时,在生产过程中希望测量值跟踪时间较短,则应该缩短积分时间,回复时间长的生产过程则应该有较长的微分时间。
(1)、比例、积分调节
a)、积分时间置于最大
b)、微分时间切除
c)、按下述方法寻求比例度的最佳值。把比例度从较大数值逐渐往下降(例如100%→50%→20%)这时仔细观察各个比例度情况下的调节过程,直至开始产生周期性振荡。(测量值以给定值为中心作有规则得振荡),在产生周期性振荡得情况下,把此比例度逐渐加宽直至系统充分稳定。
d)、接下去把积分时间逐渐缩短,一般减少积分时间即缩短了测量值跟踪给定值得时间,但是由于过程有延迟,积分时间缩短时,仍会产生振荡,此时,表示积分时间过短,应把积分时间稍加延长,直至振荡停止。
(2)、比例、积分、微分调节
a)、积分时间置于最大
b)、微分时间置于最小
c)、和前面的比例、积分调节作用一样改变比例度,求起振点。
d)、加大微分时间使振荡停止,接着把比例度调得稍小一些,使振荡又产生,加大微分时间,使振荡再停止,来回这样操作,直至虽加大微分时间,但不能使振荡停止,以求得微分时间的最佳值,此时把比例度调得稍大一些直至振荡停止。
e)、把积分时间调成和微分时间相同的数值一般情况下是没有什么问题的,如果又产生振荡则加大积分时间直至振荡停止。
以上方法依据经验试凑法,实际应用过程中根据需要和习惯选用某一种。
4 反应曲线法
反应曲线是表达对象特性的方法之一。反应曲线法,是需要预先测量反应曲线,通过对象动态特性数据定出整定参数的方法。而在某些工艺对象上的约束条件比较严,测试有困难;而在另一些对象上,干扰因素较多,且较频繁,测试就不易准确,因此应用场合受到限制。一般现场应用较少,这里就不再多讲。
5 几种曲线的区别与判断
在实际的参数整定过程中,不论采取什么样的整定方法,理想曲线与实际曲线都存在着差别,下面介绍几种经实践总结出来的曲线与判断结果,供整定中参考。

a、 积分时间过小,振荡周期长,输出变化到指示变化时间长。
b、 比例度过小,振荡周期短,输出变化到指示变化时间短。
c、 微分时间过长,振荡周期最短,输出变化到指示变化时最短。