pid三个参数最简单的调整方法,pid先调哪个值

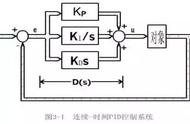
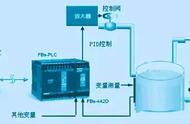
以PID控制规律构成的自动调节系统，是实现生产过程自动化的重要手段，自动调节系统控制质量的好坏直接影响着工业过程的经济性和安全性。有三种:调节器PID参数的整定方法没有被人们很好掌握，测量元件和放大器的设置不甚合理，执行机构或调节阀方面的原因。

主要讨论调节器PID参数的整定方法，首先给出控制系统的性能指标，探讨一下比例带、积分时间、微分时间对调节系统的影响，然后给出几种调节器参数的工程整定法.

1. 调节器PID参数对自动调节系统的影响图衰减曲线示意图调

1.1调节器参数的整定方法

所谓调节器参数的整定，就是选择合适的比例带、积分时间和微分时间，使自动调节系统工作在最佳的状态。

调节器PID参数的整定方法主要有:理论建模法、工程整定法。

理论建模法主要根据系统的数学模型，用控制理论的稳定判据，求得满足工艺运行的调节器参数，这种方法的缺点是需要知道或能够求出控制对象的数学模型，它要用到控制理论和数学方面的有关知识，比较复杂，不易为人们所掌握，而且理论方法求得的数学模型与被控对象的真实模型还有一定差距，正是因为如此，工程整定法深受人们的欢迎。

1.2控制系统性能指标

衡量控制系统工作优劣的依据是控制系统的性能指标：

衡量控制系统工作优劣的依据是控制系统的性能指标，这里我们给出两个指标有1/4衰减曲线或衰减率Ψ=0.75.

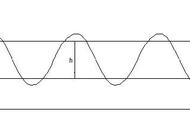
如图1所示:a为第一个波峰的高度，b为第二个波峰的高度，1/4衰减曲线为:

第二个波峰的高度/第一个波峰的高度=b/a=1/4；

衰减率Ψ=（a-b）/a=0.75.

图1:1/4衰减曲线示意图

对于反应较快的对象，例如锅炉给水流量、管道压力、汽包液位、炉膛负压等，要严格看出1/4衰减曲线或Ψ=0.75衰减率是困难的，这时，往往只能定性的识别，以波动次数为准，对于要求衰减率Ψ=0.75的系统，一般以向上二波动二次，向下波动一到二次为宜。

2.δc*Ti最小。即比例带和积分时间的乘积最小，上述指标中的第1条，是系统稳定的必要条件，一般地，按Ψ=0.75求出的调节器参数往往不只一组，若要控制系统有好的稳态品质，又有好的暂态品质，即扰动曲线能稳、准、快地接近原来的状态，还须有第二个条件δc*Ti最小。

1.3比例带.δc、积分时间Ti、微分时间Td对系统控制过程的影响

1.比例带和比例作用

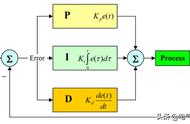
图2比例作用框图

比例作用是指调节器的输出和输人偏差成正比，如图2所示

△C=Kp*△e=（1/δc）*△e

式中△e、△C分别为比例调节器的输入偏差和输出，δc为比例带，Kp为放大倍数，比例带与放大倍数互为倒数，即δc*Kp=1

由上式可知，δc大时，1/δc小，若有偏差，△C变化较小，即比例带大时，比例作用微弱，系统达到稳定需要的时间较长，系统的稳定性好反之，δc小时，1/δc大，若有偏差，△C变化较大，即比例带小时，比例作用强，系统达到稳定需要的时间较短，系统的稳定性差.

一般地,当调节器输出变化很小而引起被调量变化较大时,应将比例带置于较大的数值； 当调节器输出变化很大而被调量变化很小时,应将比例带置于较小 的数值。 事实上,比例作用可对动态偏差进行粗调,使大偏差减小或将偏差控制在较小范围内。

比例作用可 以总结如下：

比例带消动不消静；

大者衰减,小者发散；

大则调节时间长,稳定性好；

小则调节时间短,稳定性差；

被量变化小时宜置小,大时宜置大；

注； 动指动态偏差,静指静态偏差

2. 积分时间Ti和积分作用

积分作用主消静；

大则调节时间长，稳定性好；

小则调节时间短，稳定性差；

对象滞后小时宜置小，大时宜置大；

3.微分时间Td与微分作用

微分作用对调节过程 的影响可 以总结如下:

微分作用提前动;

大则调节时间短,稳定性差:

小则调节时间长,稳定性好:

对象滞后小时宜置小,大时宜置大:

总之,比例主要用于偏差的“粗调”,保证控制系统的“稳”;

积分主要用于偏差的“细调”,保证控制系统的“准”:

微分也主要用于偏差的“细调”,保证控制系统的 “ 快 ”

2.调节器参数的整定

2.1 经验法

它的基本思路是:根据经验.确定一组调节器参数 ，并将系统投人闭环运行,然后人为地加阶跃扰动,观察被调量的阶跃响应曲线 ，若认为控制质量不满意,则根据调节器参数对控制过程的影响改变参数的设置,直到满意为止.具体步骤 如下：

①　调节器 积分时间Ti→ꝏ、微分时间Td →0， 控制系统投入闭环运行,由大到小改变比例带δc， 用给定值做扰动信号 ，观察控制过程 ，直到出现衰减曲线为止.

②　将比例带增大1.2倍,由大到小改变积分时间Ti,同样,观察阶跃扰动曲线,直到得到满意的控制过程.

③　积分时 间不 变,改 变 比例带,观察控制过 程,如有改变,则 继续调 整,直 到满意为止,否 则 ，比例带 不 变,再 调 整 积 分时 间,力 求改 善控制过程,如此反 复凑试,直到找到满意 的 比例带和积分时 间为止。

④　引人微分 时 间 兀,微 分时间取 积 分 时 间 的1/3~1/6 一之 间,和前述步骤类似,微分时间也需反复调整,直到满意为止。

注意： 试凑过程 中应使Td/Ti的值尽量保持不变,以保证调节器干扰系数不变

2.2等幅振荡法

①　按纯 比例系统整定： 比例带δc→ꝏ、,调 节器 界、 积分时间Ti→ꝏ、微分时间Td →0，控制系统投人 闭环运 行,由大到小改变 比例带 占 。,直到 出现 等幅振 荡 曲线,此时的 比例带称 为临界 比例带,用Pk来表 示,振荡周期称为临界周期,用Tk来表示。

②　按表1 计算 δc、Ti 、Td 参数的具体数值。

③　按上述数值整定,投入运行,再观察调节过程的变化 若超调量太大,过渡过程时间较长 ，则可适当减小比例带和积分时间,效果就会好些.

表1等幅振荡法和衰减曲线法参数选择

2.3衰减曲线法

①　按纯比例系统整定：比例带V→ꝏ，调节器Ti→ꝏδc ，Td→0，待系统稳定后,逐步减小比例带，直到出现1/4的衰减曲线，假设此时的调节器比例带为PS,振荡周期为TS .

②　按表1计算δc、Ti、Td 数值.

③　整定δc、Ti、Td 参数，观察调节过程曲线，曲线不理想时，可适当进行调整.

3.结束语

本文介绍了自动调节系统的性能指标，分析调节器的比例带、积分时间、微分时间对调节过程的影响，并给出了三种调节器参数的整定方法，经验法简单可靠，但须有一定的整定经验,易带有主观片面性。等幅振荡法适用于允许作临界振荡实验的系统,对那些被控对象时间常数和滞后较小的系统,一 般不允许进行临界实验,所以不能使用等幅振荡法；衰减曲线法适用于控制对象时间常数较大和滞后较大的系统,对于扰动频繁的系统,往往得不到闭环运行的阶跃响应曲线,这时采用衰减曲线法不容易得到满意的结果,因此,要根据控制对象的具体情况,选择合适的整定方法。

经验参数与口诀

温度控制系统：P=20-60% I=180-600s D=30-150s

流量控制系统：P=40-100% I=6-60s

压力控制系统：P=20-60% I=24-180s

液位控制系统：P=20-60% I=60-300s

参数整定找最佳，从小到大顺序查

先是比例后积分，最后再把微分加

曲线振荡很频繁，比例度盘要放大

曲线漂浮绕大湾，比例度盘往小扳

曲线偏离回复慢，积分时间往下降

曲线波动周期长，积分时间再加长

曲线振荡频率快，先把微分降下来

动差大来波动慢，微分时间应加长

理想曲线两个波，前高后低4比1