三年级学生初学“周长”的重点是什么
2018年12月1日星期六
本文主要续写前文《“运动场”和“跑道”是一回事吗》中的题(3)的辨析。
题(3)如下:
“
(3)一个封闭图形上所有线段长度的总和就是这个图形的周长。 ( )
”
此题依然出现了“对”与“错”的分歧。进一步对主张“错”的原因进行梳理,又可分为两类意见。为了下文叙述之方便,以“对1”、“错1”、“错2”指代三种观点,指代词不暗示任一观点本身,因为每种观点都是有价值的。本文亦不追求读者划一地接受其中某种观点,更期望给予读者取舍之帮助。
一“错1”方认为此题的错误在于“线段”一词,若是改为“边”,便是正确的。如下:
(3)一个封闭图形上所有边的长度的总和就是这个图形的周长。 ( )
这样做的原因大抵有二:一是封闭图形的“边”不见得必是“直的”线段,也可以是规律的“弧线”,甚或是散漫的“曲线”;二是“边”这个词暗含了“外围的”、“一周的”意思,紧扣“周长”的概念:封闭图形一周的长度,是它们的周长。

多种多样的封闭图形
这种观点将题(3)的考察重点引向“封闭图形的辨识”。
二“对1”方则认为:题(3)的考察重点应当是让学生感悟“周长”的最基本的、最朴素的算法应当来自于“周长”概念本身,也即“单纯地用加法”就可以完成计算。至于所谓“长方形、正方形的周长计算公式”:

长方形和正方形的周长计算公式
只不过是窄范围内的凑巧总结罢了,比如应用了“对边相等”、“四边相等”这样的恰如其分的特点,大多情况并不见得如此。这种观点将题目的关键词锁定在“所有”、“长度的总和”上。
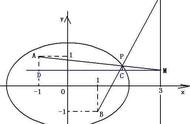
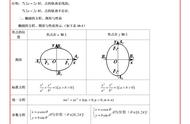
长远地来看,有价值的“周长计算公式”当属“圆和椭圆的周长计算公式”。如下:

圆和椭圆的周长计算公式
(其中:a是椭圆的半长轴,b是椭圆的半短轴)
显然,这是基于“曲线”的规律性和“曲线”的测量困难。两条公式中都出现了神奇的圆周率π,且不论其是个什么东西,单看其作用就够让人惊讶地“大吃几斤”的:π沟通了“规律曲线”和“直线段”之间的关系,使得不便测量的曲线问题变为可以方便测量的直线段,比如圆的直径、椭圆的长轴和短轴,突显了“计算”的重要地位,因为“长度”单靠“测量”去完成,是存在短板的。一个极简单的例子是:地月距离就别指望用“尺子测量”出来。
“长方形和正方形的周长计算公式”的价值微乎其微,其只不过是基于“基础加法”的一种算法的简化和优化。这样的优化不具备更广阔的生命力,且仍会使小学生在一定阶段里付出一些“代价”。令人头痛的是,用乘法优化加法后,会掩盖 “一维长度用加法,二维面积用两个长度作乘法”的计算本质。常见的错误是:使小学生混淆“周长”和“面积”的计算,因为二者都有“乘法”参与,哪怕将歌诀“周长一条线,面积一整片”背得滚瓜烂熟,依然会执着地出现错误。以至于我突发奇想:“周长”就彻头彻尾、老老实实地用加法计算吧,“算法优化、升级”一事,烦够了,或许就会自我开窍。
(重要程度★★★★)
以下是两个真实事例。
一是计算一个边长为4厘米的正方形的周长。如果用:4×4,许多学生并不能回答出两个“4”的不同意义,比如:一个4表示“正方形每条边的长度是4厘米”,另一个4表示“有4条相同的边”。或许,他们在“思维”上是理解的,但就是不会准确地组织语言,卡在了语言关上。但是,“我会想,只是不会说”、“我明白,只是说不出”,听来似乎更像是笑话。如果改用:4+4+4+4,提问“4个加数表示的意义相同吗?”、“4代表什么?”,则回答效果好了许多。但我并没有进行“独立、分组教育实验”,或许“先问乘法后问加法”的提问方式亦带来了许多干扰和答题经验暗示,准确效果难以量化。“同水平”学生样本群体的选取、初学阶段的时间点的把握、多次实验等都是可以想到的困难。
二是一个罕见的个例,但对我触动极深。一次家庭作业中,我布置了一道“测量并计算周长”的题,其中有一个是三角形。第二天,我发现一个学生唯独把这个“三角形”的周长没做,询问得到的答案是:“我妈妈说三角形没有周长计算公式,不能套公式计算。”这便是对“生搬硬套”的生动诠释!亦让我坚信:小学生初学“周长”的重点在于理解“周长”的概念,牢固树立“一周长度之和”的核心理念,而不是将基于优化算法的公式,用应试训练的手段做到极致,颠倒本末,喧宾夺主。
(重要程度★★★★★)
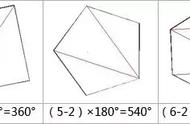
三“错2”方的观点最让人迷惑。这种观点认为:题(3)的错误出在方位词“上”上。(呵呵,“上上”是谁?多别扭的读法!)依据是细心的“错2”方老师认为,这个方位词“上”会加剧小学生对下面题型的误解。