阿基米德在他的著作《关于圆锥体和球体》中计算了一个椭圆的面积(命题4)。
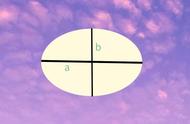
当我们垂直地缩小一个圆时，我们得到一个椭圆。椭圆有一条长半轴和一条短半轴。
椭圆面积的公式是对圆面积的一种美丽的推广。长半轴a、短半轴b的椭圆面积为:
首先，我们用直观的方法推导出这个公式。但阿基米德的“方法”和严格的定理证明之间有明显的区别。
之后，我们将解释阿基米德是如何证明这个结果的。
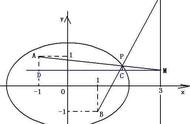
在椭圆周围半径为a的圆称为它的辅助圆。如果我们(垂直地)缩小这个圆，我们得到一个椭圆。给定椭圆上的点m，它满足关系式:
高中数学椭圆公式大全（高中数学椭圆秒杀公式）
阅读全文>>2022-10-28 11:23:39
椭圆形面积计算公式（椭圆长50米宽40米面积多少）
阅读全文>>2022-10-28 10:57:45
椭圆的面积怎么求（椭圆面积是怎么算出来的）
阅读全文>>2022-10-28 11:01:21
锐界st如何讲亮点（锐界st参数配置）
阅读全文>>2022-10-28 11:06:09
锐界st进口版能买到吗（锐界st优惠多少钱）
阅读全文>>2022-10-28 11:01:41
定积分求椭圆面积（椭圆封头面积计算公式）
阅读全文>>2022-10-28 11:00:16
正方形里边是椭圆形该怎么求面积（正方形中间一个椭圆形求面积）
阅读全文>>2022-10-28 11:10:30
用极坐标求椭圆面积（极坐标二重积分求椭圆面积）
阅读全文>>2022-10-28 10:50:00
椭圆的周长公式（椭圆必背的十大结论）
阅读全文>>2022-10-28 11:19:42
椭圆面积公式和例题（椭圆面积公式的几种推导方法）
阅读全文>>2022-10-28 11:07:13
