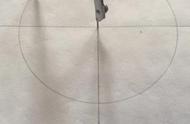
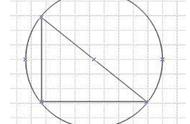
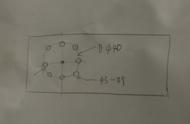
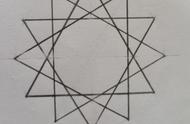
此时我们就可以发现,如果让这个圆的圆心与这个等边三角形的一个顶点重叠,那么这个圆中就恰好可以放下6个这样的等边三角形。

实际上,这样的规律适用于任何一个圆,换句话来讲就是,任何一个圆都可以恰好放下6个与之半径相等的等边三角形,由于古巴比伦人使用的是“六十进制”,因此他们就认为每个等边三角形的底值为60,6个等边三角形加起来就是360,而这就是“圆是360度”这种设定的起源。
需要注意的是,以上所述只是一种认同度相对较高的观点,除此之外,人们对此还提出了多种不同的说法,例如有人认为“圆是360度”这种设定,应该是古人通过观察太阳在天空中的运动轨迹得出的,也有人认为这种设定应该是古人根据太阳的视直径与天球视周长的比例得出的,这里就不一一说明了。
那么问题就来了,在人类普遍使用了“十进制”之后,为什么还是会使用“圆是360度”这种设定,而不是使用更简单的数字,比如说100度?其实答案很简单,尽管“100”这个数字相对来讲更简单,但它却不是最适合等分的自然数。
在讨论与圆有关的几何问题时,我们通常会将圆进行等分,其中最常见的就是二等分、三等分、四等分,假如我们将圆设定为100度,那么它在三等分的时候,就会出现33.333……这样的循环小数,这无疑就使问题复杂化了。

然而假如我们将圆设定为360度,就可以简单处理了,因为这个数字可以被2、3、4整除。

实际上,360其实是一个“高度合成数”,我们可以将其简单地理解为,在小于等于360的所有自然数之中,可以将360整除的自然数是最多的,比如说在1至10的范围内,除了“7”之外,360可以被其他的任何自然数整除。
可以看到,这种优势是小于360的其他任何自然数都无法比拟的(包括100在内),当然了,比360更大的“高度合成数”(比如720)可以被更多的自然数整除,但使用这样的数字又会因为数值过大而在另一个层面上使问题复杂化。
综合考虑之下,360这个数字既不是很大,又可以被尽可能多的自然数整除,所以如果我们将圆设定为360度,就可以更加方便地讨论与圆有关的几何问题,正是因为如此,“圆是360度”这种设定才被人们普遍使用,并一直沿用至今。
好了,今天我们就先讲到这里,欢迎大家关注我们,我们下次再见。
(本文部分图片来自网络,如有侵权请与作者联系删除)
,