2021-4-23是个特殊的日子。世界读书日遇上了中国海军建军节。祝中国人民海军72岁生日快乐!
在这一天,收到了网购的《数学杂谈》(张景中院士献给数学爱好者的礼物),迫不及待的开卷有益,果然受益匪浅。
分享一下书中的一个精彩段落:巧分生日蛋糕。
一块正方形的生日蛋糕(严格地说,是正四棱柱形的。由于这柱体的高相对较小,通常人们把它叫做方形蛋糕),表面上涂有一层美味的奶油,要均匀地分给5个孩子,应当怎么切呢?
困难在于,不但要把它的体积分成5等份,同时要把表面积也分成5等份!
要是4个人分、8个人分就好了。不然,要是圆形的蛋糕,也就好了。偏偏是方形蛋糕5个人来分!
且慢抱怨!冷静地想一下,你会意外地发现,“方形”和“5人来分”这两个条件,并没有给你增加什么困难,解答是令人惊奇地平凡而简单:只要找出正方形的中心O,再把正方形的周界任意5 等分;设分点为A,B,C,D,E,作线段OA,OB,OC,OD,OE, 沿这些线段向着柱体的底垂直下刀,把它分成5个柱体便可以了。如图1-18,便是一种分法。(我们在图中标出了方形各边的5等分点,这就易于看出A,B,C,D,E是周界的5等分点了。)
要证明这种分法的正确性,只要用一下三角形面积公式和柱体体积公式就够了。由于中心O到4边距离相等,所以图中用虚线划分的小三角形都是等底等高的!剩下的,就是用人人皆知的公式,通过具体计算验证各块的体积相等,并且所附带的奶油面积也相等罢了。
图片

图1-18
这件事提醒我们:面对貌似困难的题目不要紧张,冷静下来,用你学过的基本知识去分析它,往往会发现它其实并不难。
让我们进一步想想:如果蛋糕是正三角形,或者是正六边形、正n边形,而且是m个人来分呢?你一定会毫不犹豫地回答:分法是一样的!
如果蛋糕是任意三角形的呢?也许你不那么有把握了吧!想一想:刚才能成功的关键是什么?是“方形中心到各边等距”。那么,三角形内有没有到各边等距的点呢?有,内切圆心就是!分法找到了:把三角形的周界分成5等分,把分点A,B,C,D,E分别和内心O连起来,沿这5条线段下刀就是。
但是,你会把任意三角形的周界5等分吗?这时,图1-18中先把各边5等分的办法显然不太适用了。你可以先把3边“拉”成一条线段,分好之后再搬回来。用规尺完成这个作图是容易的,如图1-19所示,这里不再用文字解释了。
图片
图1-19

图1-19
刚才我们用到了三角形的内心,这会使我们想到:任意的圆外切多边形也有“内心”,即它的内切圆心O;而O到外切多边形的各边也是等距的。这样一来,所有的圆外切多边形的蛋糕,都可以按照要求均分成m块了。方法仍然相同,比如,菱形蛋糕便可以这样来分。
通常吃的蛋糕的形状大致都是柱体的。如果一家食品公司别出心裁,做了一种金字塔形蛋糕,我们能够把它(连同它的表面积)均分成5块吗?

图1-20
金字塔形,就是正四棱锥形。它的分法仍然和前面的分法雷同。只要找出锥形的底的周界的5等分点,设分点为A,B,C,D,E ,把它们和锥顶点O连接起来。如图1-20,设O在锥底的正投影为O′,我们以△OO'A,△OO'B,△OO'C,△OO'D,△OO'E为剖面下刀,便可以满足要求了。
进一步思考,你会想到:如果棱锥的底面是圆外切多边形,而且棱锥顶点和底的内切圆圆心连线垂直于底面的话,仍可以依样画葫芦地均分成若干块。因为,利用勾股定理和立体几何里的“三垂线定理”容易验证:棱锥各侧面三角形的高相等。另外,底面内心仍和底的各边等距。
回顾一下,我们从开始到现在,一步一步已走得不近了;但每步并不太费力。这样一小步一小步地向前挪动,可以使你从简单情况出发,解决相当困难的问题。不信,你可以试问一位爱好数学的朋友:
“怎样把正四面体形的蛋糕均匀地分成5块,同时使表面上的奶油也分得均匀?”
十之八九,他会觉得这是个难题。甚至他很难一下子相信你告诉他的解答(如上述)是正确的!但对于你,这个问题已了如指掌了。
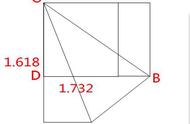
但是,这样的分法并非无往而不胜!如果是一块长和宽不相等的矩形蛋糕,就会让我们碰钉子。不过,也不是没有办法。设矩形的长为a,宽为b,下面提供的方法可以把它均分成5块(如图1-21)。注意,别忘了表面积也要分均匀。
图片
图1-21