大家好!我是小刘同学!今天继续对三角形的学习,分享一道中线相关的题目。
请看题:在△ABC中,AB=AC,AC边上的中线BD把△ABC的周长分为12cm和15cm两部分,求△ABC的各边长。
在以前的分享中,我在《壁虎的偷袭》一文介绍了“数形结合”思想,在《数学:三角形的三边关系(2)》一文又介绍了代数思维与“分类讨论”思想,现在可以综合三者来解决这道题目。
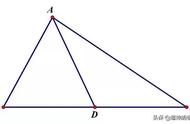
仔细读题,并根据题意作出图形,帮助理解与思考。题中第一条实用的已知条件是“在△ABC中,AB=AC”,等边对等角,我们就知道首先这肯定是一个等腰三角形。

接下来那又该如何理解题中第二条实用的已知条件“AC边上的中线BD把△ABC的周长分为12cm和15cm两部分”?我们知道,中点是把一条线段分成两条相等线段的点,而连接三角形一个顶点和它的对边中线的线段叫做三角形的中线。结合题意,则AD=CD,且是AB=AC=AD CD,进而得出AB=2AD=2CD。
三角形一边上的中线把原三角形一定分成两个面积相等的小三角形,依据正是我们所熟知的三角形面积公式:面积=底×高÷2(S=½ah,其中a是三角形的底,h是底所对应的高),且因三边均可为底,所以对该公式的正确理解即为——三边与之对应的高的积的一半是三角形的面积。由此判断所分成的小三角形的底与高也是不会改变的,可见面积相等。

但是,它们的周长不会相等、形状也不会相同。结合题意,因为中线BD将△ABC的周长分成两部分:(BC CD)和(AD AB),无法确定谁为12cm,谁为15cm,就是说这里将会产生两种情况,必须分类讨论。如图所示,即:
情况一,AB AD=12cm且BC CD=15cm;
情况二,AB AD=15cm且BC CD=12cm。

再使用设未知数x的方法,比如我们就可设AD为x,则 AD=CD=x,AB= 2x,从而列出方程:
情况一,因为AB AD=2x x=12cm,得出x=4,所以AB=AC=2x=2×4=8,则AD=CD=4;又因为BC CD=15cm,BC=15-CD=15-4=11,所以最后得出的结果是△ABC各边长分别为AB=AC=8,BC=11。我们要通过三角形的三边关系判定原理(见我分享《数学:三角形的三边关系》一文)来论证该三角形是否存在,即AB AC>BC,且AB-BC<BC,则此时8 8=16>11,且8-8=0<11,三角形存在。
情况二同理,因为AB AD=2x x=15cm,得出x=5,所以AB=AC=2x=2×5=10,则AD=CD=5;又因为BC CD=12cm,BC=15-CD=12-5=7,所以最后得出的结果是△ABC各边长分别为AB=AC=10,BC=7。我们再通过三角形的三边关系判定原理来论证该三角形是否存在,即AB AC>BC,且AB-BC<BC,则此时10 10=20>7,且10-10=0<7,三角形存在。
综上所述,△ABC的三边长分别为8cm,8cm,11cm或10cm,10cm,7cm。
谢谢大家,下回再见!
,