提要
三角形中位线是三角形中重要的线段,三角形中位线定理是一个重要性质定理,它是前面已学过的平行线,全等三角形,平行四边形等知识内容的应用和深化,对进一步学习非常有用,在判定两直线平行和论证线段倍分关系时常常用到。在三角形中位线定理的证明及应用中,处处渗透了化归思想,它是一种重要的思想方法。
知识全解
一.定义
连接三角形两边中点的线段称为三角形的中位线
提示:
三角形的中位线与三角形中线是两个不同的概念,三角形中线是三角形一边中点与折条边所对的顶点的连接线段。
二.性质
三角形中位线平行于第三边,并且等于第三边的一半。
方法点拨
类型1 求角度
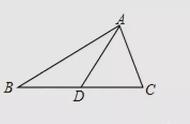
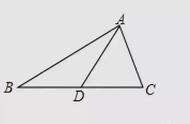
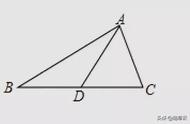
例1 如图所示,在△ABC中,D,E分别是AB,AC的中点,∠B=50度。先将△ADE沿DE折叠,点A落在三角形所在平面内的点为A1,则BDA1的度数为___

【分析】由折叠的性质可知AD=A1D,根据中位线的性质得DE‖BC,再根据平行线性质计算角度
【解答】∵D,E分别是边AB,AC的中点
∴DE‖BC
∴∠ADE=∠B=50度
又∵∠ADE=∠A1DE
∴∠A1DA=2∠B
∴∠BDA1=180-2∠B=80度
【点评】本题将三角形中位线定理与折叠问题结合起来了,解题关键是抓住折叠前后图形全等。
类型2 根据三角形的中位线证明
例2 如图所示,在四边形ABCD中,对角线AC,BD相交于点O,且AC=BD,E,F分别是AB,CD的中点,EF分别交BD,AC于点G,H。求证:OG=OH

【分析】取BC边的中点M,连接EM,FM,则根据三角形的中位线定理,即可证得△EMF是等腰三角形,根据等边对等角,即可证得∠MEF=∠MFE,然后根据平行线的性质证得∠OGH=∠OHG,根据等角对等边即可证得。
【解答】取BC边的中点M,连接EM,FM
∵M,F分别是BC,CD的中点
∴MF‖BD,MF=1/2BD
同理:ME‖AC,ME=1/2AC
∵AC=BD
∴ME=MF
∴∠MEF=∠MFE
∵MF‖BD
∴∠MEF=∠OGH
同理,∠MEF=∠OHG
∴∠OGH=∠OHG
∴OG=OH
【点评】在解答多中点问题时,如果无法直接运用三角形中位线定理,可以再取中点,构造三角形中位线解答。
,