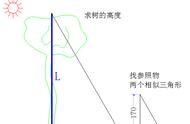
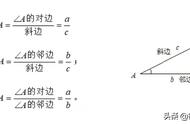
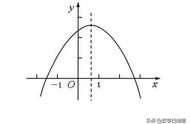
八年级,函数出现了。
看不懂定义,不明白表达式,不理解图象,不会做题;一学期结束了,对函数仍是一知半解的学生绝对不在少数。
而实际上,函数入门只需要明白两个问题:
1、函数到底是什么,它是干什么用的;
2、函数(特别是一次函数)表达式和其图象之间有什么关系。
明白了这两点,我敢肯定,你将一顺百顺,一路顺到毕业。
接下来,请把看小说的劲头拿出来,十分钟后你就会惊奇地发现:函数,你懂了!
函数是什么,有三种理解方式:
1、最直观的说法:
在中学阶段,大多数情况下,函数都是以一个等式的形式出现的,等号的左边是一个单独的字母y,右边是一个关于x的代数式。例如:y=2x+1,y=3x,y=x²等等都是函数。
这种说法虽然很不严谨,但先给函数一个这样的直观印象总比一点儿头绪都没有要好得多。
2、最有用的说法:
函数可以看作是一系列点的横、纵坐标之间的规律。

这些点的共同特征是:纵坐标都是横坐标的2倍;用x表示横坐标,y表示纵坐标,则这些点的坐标都符合规律y=2x,等式“y=2x”就是一个函数。
由此我们可以说,函数就是一个规律,它是用来表示一组点的横纵坐标之间的关系的。
把满足纵坐标是横坐标2倍的所有点都写出来是不可能的,但我们可以使用“y=2x”这样一个简单的函数就可以做到,这就是函数最闪光的地方。
这个等式“y=2x”称作函数的表达式,有了这个表达式,咱们就可以很方便地求出上面那组点中的任何一个,例如,令x=8可得y=16,则点(8,16)就在这组点中。
可能你会有疑问,没有表达式我也知道(8,16),(9,18)等等这些点都在上面那组点中。
这是因为咱们举的例子比较简单,在实际应用中,表达式会复杂得多,例如:

3、最准确的说法:
在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数。
这是课本上给出的函数的定义,虽然难懂,但它最准确,它是判断函数的依据。
掌握函数的这个定义,你只需要记住下面这句话:
在列表中、在图形中或者在一个等式中,只能有两个变量x和y,当x取任意一个可以取的值时,y只能得到一个值,则y就是x的函数。

到此为止,我们对函数的概念应该有所了解了,但知道这些对我们做练习的作用并不太大。
接下来的内容是针对如何做题的,它是一次函数整章的核心,懂了它,你就什么都懂了。
如下图,为了描述这组点:…、(0,0)、…、(2,4)、…、(3,6)、…、(4,8)、…,可以使用下面的三种方法:1、表格;2、表达式;3、图象。