①正弦
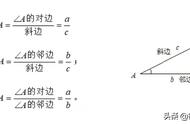
三角函数一般都从正弦开始讲起,下图是一个直角三角形。c是斜边,两条直角边分别为a,b.
sinA表示∠A的正弦值,而它的正弦值等于对边比斜边。比如:sin30°=对比斜=1/2,(在直角三角形中,30°对应的直角边是斜边的一半)

②余弦
cos表示余弦,cosA=邻比斜=b/c
细心的小伙伴会发现∠A的余弦正好表示∠B的正弦
没错,在同一直角三角形中,∠A+∠B=90°,那么,sinA=cosB,cosA=sinB。
且sin²A+sin²B=1
注:(a/c)²+(b/c)²=(a²+b²)/c²,由勾股定理得:a²+b²=c²,所以原式值为1

③正切
正切用符号tan表示,tanA=对比邻=a/b

④余切
余切用cot表示,cotA=邻比对=b/a
同一角的正切余切积为1,现在教材一般不讲余切,只有正弦,余弦和正切。这个大家了解就好

如图所示,我国两艘海监船A,B在海南海域巡航,某一时刻,两船同时收到指令,立即前往救援遇险抛锚的渔船C。此时,B船在A船的正南方向5海里处,A船测得渔船C在其南偏东45°方向,B船测得渔船C在其南偏东53°方向。已知A船的航速为30海里/小时,B船的航速为25海里/小时,问C船至少要等待多长时间才可以获救?(参考数据:sin53°=4/5,cos53°=3/5,tan53°=4/3,√2=1.41)

答案:
过点C作CD⊥AB交AB延长线于点D,则∠CDA=90°。
已知∠CAD=45°,设CD=X,则AD=CD=X,所以BD=AD-AB=X-5。
在Rt三角形中,CD=BD×tan53°,解得X=20.所以BC=CD/sin53°=25
所以B船到达的时间为25÷25=1小时
在Rt△ADC中,AC=√2X=1.41×20=28.2
所以A船到达C船的时间约为:28.2÷30=0.94小时
故0.94小时获救
,