也就是说,「一截」长6,总长25,因此需要圆形(哨塔)总个数为:
25÷6=4余1,向上取整结果为5,C选项正确。
公考中凡是涉及直线图形和曲线图形的「覆盖」的,一定和「共同交点」或者「相切」有关,关键是要理解「直曲图形覆盖」的特点。
五、例题4:学会「翻译」题*叙述【2014国考63题】一个立方体随意翻动,每次翻动朝上一面的颜色与翻动前都不同,那么这个立方体的颜色至少有几种?
(A)3
(B)4
(C)5
(D)6

一个立方体随意翻动,每次翻动朝上一面的颜色与翻动前都不同,那么这个立方体的颜色至少有几种?
(A)3
(B)4
(C)5
(D)6
正确率41%,易错项C
列出题干数据关系:
①立方体随意翻动
②翻动后颜色不同
③求颜色至少几种
本题是比较少见的和「相切」无关的推理类几何题,重点考察的是考生对题干描述的理解。
由①②可知立方体任意相邻2面颜色不同。
由③可知本题要尽量压缩颜色的种类,即在满足条件的情况下,尽可能增加每个颜色所占的面数。
想象一个空白立方体,设它的「上」面为甲颜色甲,则「前后左右」4个面都和甲面相邻,不能为甲颜色,但「下」面和「上」面相对,不相邻,根据③可以将其染成甲颜色。
同理,可设它的「前」面为乙颜色,则「上下左右」面不能为乙颜色,「后」面为乙颜色。
同理,可设它的「右」面为丙颜色,则「上下前后」面不能为丙颜色,「左」面为丙颜色。
因此本立方体上下为甲颜色、前后为乙颜色、左右为丙颜色,共有3种颜色,A选项正确。
这道题需要「翻译」,即将题干中「随意翻动、每次不同」的叙述理解成「任意相邻两面颜色不同」,这样就能够更方便解题了。本题误选C的考生,可能忽视了「至少有几种」的要求。
六、例题5:「投影」题的理解关键【2013国考62题】阳光下,电线杆的影子投射在墙面及地面上,其中墙面部分的高度为1米,地面部分的长度为7米。甲身高1.8米,同一时刻在地面形成的影子长0.9米。
该电线杆的高度是多少?
(A)12米
(B)14米
(C)15米
(D)16米

该电线杆的高度是多少?
(A)12米
(B)14米
(C)15米
(D)16米
正确率59%,易错项B
列出题干数据关系:
①电线杆影子:地面7m,墙面1m
②甲1.8m,影子0.9m
③求电线杆高度
根据②可看出甲与其影子之比为1.8:0.9=2:1
根据①可得下图:

以地面和墙的重合点(即影子在地面部分和影子在墙上部分的交点)为分界,可将电线杆分为两个部分。
下边部分投影正好到墙边,符合「物体:影子=2:1」的要求,长度为7×2=14m。
上边部分投影正好到墙上,由于电线杆和墙面都垂直于地面,因此该部分和投影长度比为1:1,即为1m。
因此答案为14 1=15m,C选项正确。
本题的解题核心在于理解「投影到墙面」的含义,理解该部分两端和墙面影子两端可形成一个平行四边形,就很容易解出答案了。这道题重在理解,计算是毫无难度的。
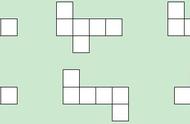
七、例题6:「视图」题不要有固定思维【2013国考75题】若干个相同的立方体摆在一起,前后左右视图都如下: