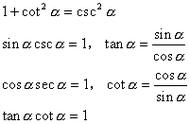仿照上述测高问题的解决方法,我们只要分别在和中使用两次正弦定理算出和,然后在中运用余弦定理算出即可.
可见,测高问题和测距问题贯穿了整个三角学的发展历程.实际上,三角学在测量领域的重要影响从其英文名“Trigonometry”就可见一斑:这个单词最早是由德国数学家毕蒂克斯(B.Pitiscus,1561~1613)于1595年首创,由希腊文“trigono”(三角)和“metrein”(测量)组合而成,其原意便是三角学的测量.各种测量问题是三角学要研究的基本问题,而后来三角学的涵义越来越丰富,逐渐成为研究三角函数及其应用的一个数学分支.
4 正、余弦定理与平面几何
有些初等几何问题用纯几何的方法求解往往比较困难,但是当我们借助正、余弦定理,则问题就可以得到简化.例如,古希腊数学家海伦在其著作《测量学》一书中提出了著名的“海伦公式”:
已知三边,记称为半周长,则三角形面积为

这个优美的公式有一个漂亮的几何论证方法,这里不再赘述.实际上,我们也可以通过正、余弦定理来对其进行推导:
已知两边及其夹角,我们有

则

由于余弦定理,可得